🌐English

逆数と平方根を求める高次収束アルゴリズム

2009-11-16
2026-01-29 改定

細田 隆之

概要

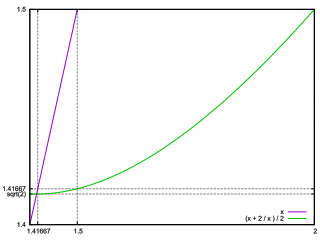
ニュートン法 (Newton-Raphson methode) は関数の 1次のテイラー近似に基づいており、単純根の近傍では 2 次収束を示す。

拡張精度や多倍長精度の計算では乗算の計算時間が支配的であるので、 目的とする桁数の計算結果を得るための乗算回数を少なくするために、 高次の収束を示す漸化式を利用するのが望ましい。 ここでは高次収束の方法を逆数や平方根の計算に適用した例を紹介する。

逆数

ニュートン法により、逆数（reciprocal）1/A を求める漸化式は、次式で与えられる。

有効桁は、繰り返しごとに 2 倍になる。

拡張精度や多倍長精度の計算では乗算の計算時間が支配的であるので、 目的とする桁数の計算結果を得るための乗算回数を少なくするために、高次の収束を示す漸化式を利用するのが望ましい。

1/A の 3次収束の漸化式

hn を導入することで、 反復誤差を明示的に表現し、級数展開によって高次の補正を導出できる。

hn を xn における誤差とする。

この方法では、各反復ごとに有効桁数が約 3 倍になる。

1/A の 4 次収束の漸化式

1/A の 5 次収束の漸化式

平方根

同様の手法が平方根の計算にも適用できる。平方根 √A のニュートン法による漸化式は次式で与えられる：

しかし、この式には A / xn の除算を行わなければならないという不利な点がある。
そこで、1/√A のニュートン法を考えてみると、より良い漸化式が得られることに気がつく。

1/√A のニュートン法による漸化式

つまり、3/2, 1/2 は定数であるので、上の式では乗算が必要とされるだけである。

√A を求めるには、B = 1/√A を求めてから、 √A = AB により √A を求める。

逆数の計算の場合と同様に高次収束の漸化式を利用するのが良い。 以下では、1/√(1 - h) の級数展開を使用している。

1/√A の 3 次収束の漸化式

h_n は、x_n の誤差と同じである。繰り返しごとに有効桁は 3 倍になる。

1/√A の 4 次収束の漸化式

1/√A の 5 次収束の漸化式

1/√A の 6 次収束の漸化式

その他の 6 次収束の漸化式

√A の 6 次収束の漸化式

1/√A の場合と同様に、√(1 - h) の級数展開を使用している。

1/∛A (= A-1/3) の 6 次収束の漸化式

1/∜A (= A-1/3) の 6 次収束の漸化式

A program example

/* _sqrt - compute the square root of x.
 * Rev.1.0 (2026-01-29) (c) 2002-2026 Takayuki HOSODA
 * SPDX-License-Identifier: BSD-3-Clause
 */
#include <math.h> /* frexp(), ldexp(), NAN */
double _sqrt(double x);
double _sqrt(double x) {
    double a, d, h;
    int    e;

    /* Lookup table for scaling factor based on exponent parity */
    static const double scf[3] = { M_SQRT2, 1.0, M_SQRT1_2 };

    if (x <  0) return NAN;     /* Return NaN for negative input */
    if (x == 0) return x;       /* sqrt(0) = 0 */

    /* Range reduction: x = d * 2^e, where d in [0.5, 1) */
    d = frexp(x, &e);

    /* Initial approximation of 1 / sqrt(d) using 3rd-order polynomial */
    /* Approximation error |err| < 5e-4 over d in [0.5, 1] */
    a = 2.605008 + d * (-3.6382977 + d * (2.9885788 - 0.9557557 * d));

    /* Scaling: convert 1/sqrt(d) to 1/sqrt(x) */
    a = ldexp(a * scf[1 + e % 2], -e / 2);

    /* Compute residual h = 1 - x * a^2, then apply correction */
    /* 6th-order convergence in final refinement */
    h = 1 - x * a * a;
    a *= (1 + h * (0.5 + h * (0.375 + h * (0.3125 + h * (0.2734375 + h * 0.24609375)))));

    return x * a; /* Return sqrt(x) = x * (1 / sqrt(x)) */
}

REFERENCES

1. K. E. Atkinson, An Introduction to Numerical Analysis, 2nd ed., Wiley.
2. IEEE Computer Society, IEEE Standard for Floating-Point Arithmetic, IEEE Std 754-2019.

SEE ALSO

• 平方根を用いた立方根の近似と複素数および拡張倍精度実数での実装例
• 算術幾何平均による円周率πの計算公式
• 整数の平方根と√(x² + y²) を求めるアルゴリズム
• √(x²+y²)を求める高次収束アルゴリズム