Higher-order convergence algorithm for reciprocal and square root

example of sqrt(2) by Newton-Raphson method
Takayuki HOSODA
November 16, 2009
Reviced May 9, 2025

The Newton–Raphson method provides a first-order approximation of a function f(x) near an estimate xn. Its convergence rate can be improved by employing higher-order approximations.

In contexts where extended- or multiple-precision arithmetic is required, recurrence formulas with higher-order convergence can significantly reduce computational cost by minimizing the number of iterations needed to reach the desired accuracy. This is particularly important in high-precision environments, where multiplication tends to dominate the overall computation time. By reducing the number of required multiplications, high-order recurrence formulas improve the efficiency of numerical methods.
The following examples illustrate such high-order methods applied to the computation of reciprocals and square roots.

Japanese Japanese edition is here.

Reciprocal

The recurrence formula for computing the reciprocal 1/A using Newton-Raphson method is given by

xn+1 = 2xn - Axn2
The number of correct significant digits doubles at each iteration.

In contexts where extended- or multiple-precision arithmetic is required, high-order convergence can significantly reduce the computational cost by minimizing the number of iterations needed to reach the desired accuracy.

Recurrence formula for 1/A with cubic convergence

With this method the number of correct significant digits roughly triples at each iteration.
Let hn be the error in xn.

hn = 1 - Axn
xn+1 = xn(1 + hn + hn2)

Recurrence formula for 1/A with fourth order convergence

hn = 1 - Axn
xn+1 = xn(1 + hn)(1 + hn2)

Recurrence formula for 1/A with fifth order convergence

hn = 1 - Axn
xn+1 = xn(1 + (1 + hn2)(hn + hn2))

Square root

Recurrence formula for √A of cubic convergence

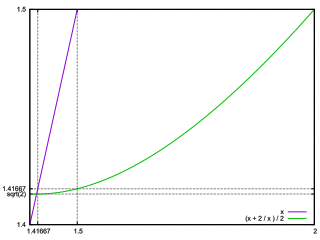
A similar approach can be applied to the square root calculation. The standard Newton-Raphson recurrence for computing √A (the square root of A) is given by:

xn+1 = (xn + A/xn)/2

However, this method has the disadvantage of requiring a division A/xn at each step, which can be computationally expensive.
Instead, if we apply the Newton-Raphson method to compute 1/√A, we can derive a more efficient recurrence formula.

Newton-Raphson Recurrence for 1/√A

xn+1 = xn(3 - Axn2)/2

Since 3/2 and 1/2 are constants, s formula only involves multiplication—making it computationally more efficient. Once 1/√A is computed, √A can be obtained simply as:

√A = A(1/√A)
As in the case of reciprocal approximation, using a higher-order recurrence for 1/√A leads to faster convergence. Below is a formula derived from the series expansion of 1/√(1 - h).

Recurrence formula for 1/√A of cubic convergence

The number of significant digits is tripled with each repetition. hn is equal to the error of xn.

hn = 1 - A xn2
xn+1 = xn (1 + hn (4 + 3 hn) / 8)

Recurrence formula for 1 / √A with quartic convergence

hn = 1 - A xn2
xn+1 = xn(1 + hn(8 + hn(6 + 5 hn))/16)

Recurrence formula for 1 / √A with 5th-order convergence

hn = 1 - A xn2
xn+1 = xn(1 + (64hn + hn2(48 + 40hn + 35hn2))/128)

Recurrence formula for 1 / √A with 6th-order convergence

hn = 1 - Axn2
xn+1 = xn(1 + hn(1/2 + hn(3/8 + hn(5/16 + hn(35/128 + hn(63/256))))))

Other recurrence formulas with 6th-order convergence

As in the case of 1/√A, we use the series expansion of √(1 - h).

Recurrence formula for √A with 6th-order convergence

hn = 1 - A/xn2
xn+1 = xn(1 - hn(1/2 + hn(1/8 + hn(1/16 + hn(5/128 + hn7/256)))))

Recurrence formula for 1/∛A (= A-1/3) with 6th-order convergence

hn = 1 - Axn3
xn+1 = xn + xnhn(1/3 + hn(2/9 + hn(14/81 + hn(35/243 + hn(91/729)))))

Recurrence formula for 1/∜A (= A-1/4) with 6th-order convergence

hn = 1 - Axn4
xn+1 = xn + xnhn(1/4 + hn(5/32 + hn(15/128 + hn(195/2048 + hn(663/8192)))))

A program example

Listing 1:
C implementation example of square root with 6th-order convergence
double _sqrt(double x) {
    double a, d, h;
    int    e;

    /* Lookup table for scaling factor based on exponent parity */
    static const double scf[3] = { M_SQRT2, 1.0, M_SQRT1_2 };

    if (x <  0) return NAN;     /* Return NaN for negative input */
    if (x == 0) return x;       /* sqrt(0) = 0 */

    /* Range reduction: x = d * 2^e, where d ∈ [0.5, 1) */
    d = frexp(x, &e);

    /* Initial approximation of 1 / sqrt(d) using 3rd-order polynomial */
    /* Approximation error |err| < 5e-4 over d ∈ [0.5, 1] */
    a = 2.605008 + d * (-3.6382977 + d * (2.9885788 - 0.9557557 * d));

    /* Scaling: convert 1/sqrt(d) to 1/sqrt(x) */
    a = ldexp(a * scf[1 + e % 2], -e / 2);

    /* Compute residual h = 1 - x * a^2, then apply correction */
    /* 6th-order convergence in final refinement */
    h = 1 - x * a * a;
    a *= (1 + h * (0.5 + h * (0.375 + h * (0.3125 + h * (0.2734375 + h * 0.24609375)))));

    return x * a; /* Return sqrt(x) = x * (1 / sqrt(x)) */
}
SEE ALSO:
www.finetune.co.jp [Mail]