2003 年 3 月 4 日
2025 年 5 月 13 日改訂
細田 隆之
English edition is here.本稿では、平方根演算のみを用いた立方根近似手法を、実数値および複素数値の入力に対して紹介します。 実数値の場合には、平方根を用いて xm/2n の形で構成された Puiseux 級数的な初期近似を用いることで、広い定義域（例：x ∈ [0.125, 4]） にわたって高精度な近似を実現しています。 さらに、3 次収束の Padé 型反復を 1 回適用することで、最終的には IEEE 754 の倍精度または拡張倍精度に対応する精度を達成します。 一方、複素数値の場合には、初期近似の構築に際し、指数 1/3 を有理数で近似し、それを平方根のネストによって xm/2n の形で表現する手法を用いています。 これにより、非常に小さい値から大きな値まで、広範なダイナミックレンジにおいて安定した収束が得られます。 これらの手法は、平方根のみがネイティブにサポートされる計算環境や、演算レイテンシを最小化する必要のある用途において、 実装の簡潔さ、数値安定性、性能のバランスを高いレベルで実現する選択肢となります。
x の平方根は x1/2 で与えられ、 x の立方根は x1/3 で与えられます。 立方根の指数 1/3 を m / 2n | m = round(2n / 3）で近似する場合、近似誤差は次式で与えられます。
m / 2n × 3 - 1その誤差は ±1/2n（負号は n が偶数の場合）となる。 具体的な値を次に示します。
これらのうち、[1e-10, 1e+10] の範囲において、初期値の近似誤差が半桁、 相対誤差で言えば ±1/√10 ≈ ±0.316 を達成するのに x11/32 が好都合なのがわかりました。1 / 2 × 3 - 1 = +0.5 1 / 4 × 3 - 1 = -0.25 3 / 8 × 3 - 1 = +0.125 5 / 16 × 3 - 1 = -0.0625 11 / 32 × 3 - 1 = +0.03125 21 / 64 × 3 - 1 = -0.015625 43 / 128 × 3 - 1 = +0.0078125 85 / 256 × 3 - 1 = -0.00390625
Fig.1: 立方根 x 1/3 を x m/2n で近似した場合の近似誤差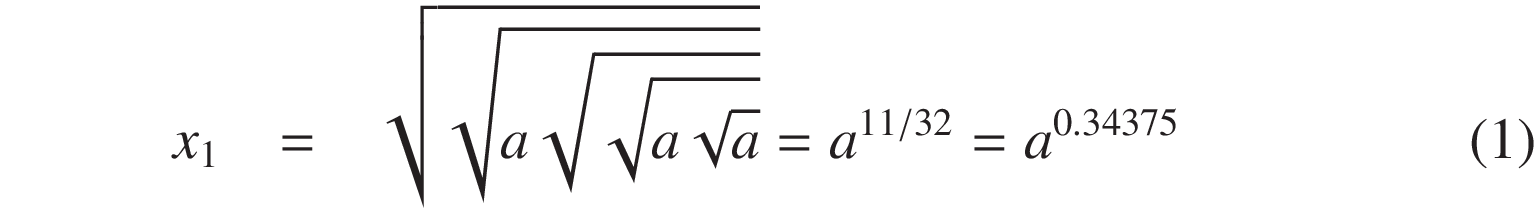
初期近似式 (1) の最大近似誤差は x ∈ [1e-12:1e+12] において、x = 1e+12 のときに約 +0.366、 すなわち約 0.437 桁の精度でしたので、後述の 3次収束の漸化式 (6) の 4回の反復によって精度が 34 倍すなわち 81 倍向上し、 0.437 × 34 ≈ 35.3 桁 > 16 桁となって IEEE 754 の倍精度に到達できることになります。
式 (1) で得られた近似値を初期値として、ニュートン法のような漸化式により立方根を求めます。
相対誤差 h の次のように定義します。![x = \sqrt[3]{a}](eqn-cbrt-a.png)
立方根関数 x1/3 は x ≠ 0 において無限級数に展開できるので、 (1 + h)1/3 は次の級数展開で表せます。
より効率的な反復式を得るために、この級数を (1, 1) パデ近似 (Padé approximation) に置き換え、1次と 2次の係数が級数展開の係数と一致するようにします。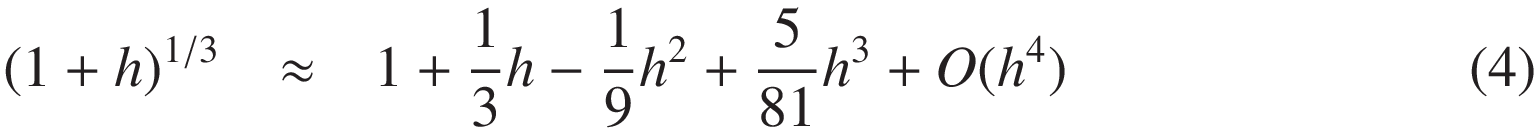
式(3)と式(5)から、以下の漸化式が導かれます。
解の近傍では、ニュートン・ラフソン法は 2次の収束を示しますが、 (1, 1) パデ近似による漸化式は 2次の項まで級数展開と一致するため、 この漸化式は 3次の収束を示します。
また、ニュートン・ラフソン法では、初期推定値が真値から離れている場合に不安定になることがありますが、 このパデ近似による漸化式では、そのような場合にも優れた数値的安定性を示します。 導出過程は異なりますが、この漸化式は Halley's method によるものと等価です。この方法は a の n乗根 (ただし a ≠ 0) にも拡張でき、次の 3次収束の漸化式が導かれます。
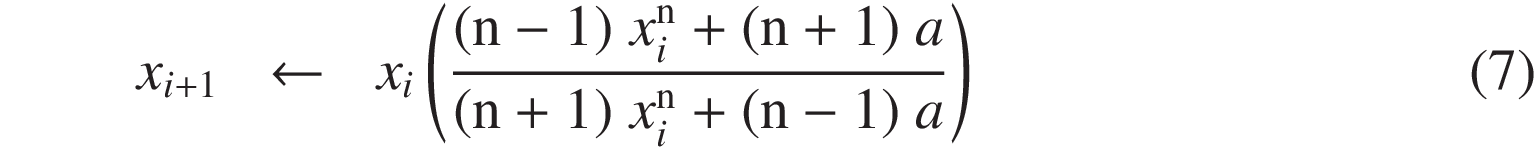
また、パデ近似の次数を (2, 2) または (3, 3) にした場合にも、式 (6) と同様に、以下の漸化式 (8)、(9) が導かれます。 それぞれの漸化式は、5次および 7次の収束を示します。
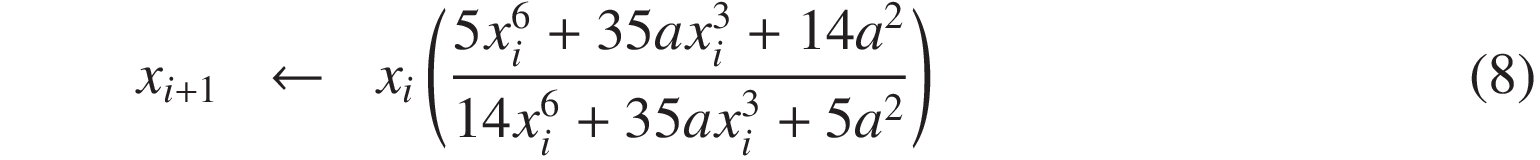
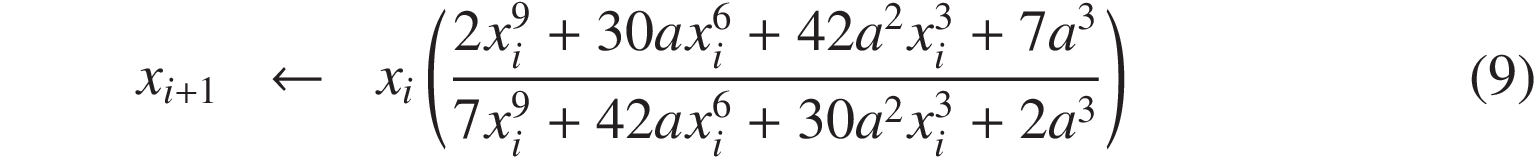
Fig.2: cbrt 初期近似誤差とその収束挙動 (IEEE 754倍精度環境での計算）
使用計算式初期近似：3次収束の漸化式：
Listing 1:
cbrt - for HP 42SListing 2:
ccbrt - complex cube root function in C9900 { 68-Byte Prgm } 01▸LBL "cbrt" 02 ABS 03 X=0? 04 RTN 05 LASTX 06 ENTER 07 ENTER 08 ENTER 09 SQRT 10 × 11 SQRT 12 SQRT 13 × 14 SQRT 15 SQRT 16▸LBL 00 17 ENTER 18 ENTER 19 X↑2 20 × 21 ENTER 22 + 23 LASTX 24 RCL+ ST T 25 RCL+ ST T 26 X<>Y 27 RCL+ ST T 28 ÷ 29 X<>Y 30 × 31 LASTX 32 RCL÷ ST Y 33 1 34 - 35 ABS 36 1?-11 37 X>Y? 38 GTO 01 39 R↓ 40 R↓ 41 GTO 00 42▸LBL 01 43 R↓ 44 R↓ 45 RTN 46 .END./* REFERNCE ONLY: FOR EXPLANATION OF THE ALGORITHM AND NOT INTENDED FOR ACTUAL USE. */ #include <complex.h> #include <math.h> #include <float.h> double complex ccbrt(double complex x); /* The ccbrt(x) function compute the cube root of x. */ /* ccbrt Rev.1.5 (May 13, 2025) (c) 2003 Takayuki HOSODA */ double complex ccbrt(double complex a) { double complex x, xp, c; double r, rp, s; int e; if (a == 0) return 0; /* Simple range reduction */ #ifdef USE_FREXP frexp(cabs(a), &e); x = a * ldexp(1.0, -e + e % 3); s = ldexp(1.0, e / 3); #else x = a; s = 1.0; while (cabs(x) < 0x1.0p-195) { x *= 0x1.0p+195; s *= 0x1.0p-65; } while (cabs(x) > 0x1.0p+195) { x *= 0x1.0p-195; s *= 0x1.0p+65; } while (cabs(x) < 0x1.0p-39) { x *= 0x1.0p+39; s *= 0x1.0p-13; } while (cabs(x) > 0x1.0p+39) { x *= 0x1.0p-39; s *= 0x1.0p+13; } #endif /* Initial approximation by x^(11/32) and range expansion */ x = csqrt(csqrt(x*csqrt(csqrt(x*csqrt(x))))) * s; r = 0x1.0p+39; do { /* Asymptotic formula */ xp = x; rp = r; c = x * x * x; #if defined( USE_SEVENTH ) x += x * (a - c) * (5 * (a * a + c * c) + 17 * a * c ) / (a * a * (a + a + 30 * c) + c * c * (42 * a + 7 * c)); #elif defined( USE_FIFTH ) x += 9 * x * (a + c) * (a - c) / (14 * c * c + 35 * a * c + 5 * a * a); #else x += x * (a - c) / (c + c + a); /* Cubic convergence */ #endif r = cabs(x - xp); /* Correction radious */ } while (r != 0 && rp > r); /* Convergence check by Urabe's method */ return x; }注：実用には例外処理とレンジ・リダクションが必要かも知れません。
ダウンロード : cbrt.raw — (Free42 用 raw プログラムファイル)
実数の範囲において sqrt 関数の他に、実数の指数部を直接扱う関数 ldexp, frexp が使える環境の場合には、レンジ・リダクションが簡単になります。
平方根、すなわち 1/2 のべきを用いた ピュイズー級数 (Puiseux series) 的な近似を用い、 レンジ・リダクションによる [0.125, 4] の範囲において最適化した 3 項の初期近似式 (10) を下に示します。
初期近似式 (10) の最大近似誤差は 約 0.009、すなわち約 2.04 桁の精度でしたので、 前述の 3次収束の漸化式 (6) を 2 回適用すれば 2.04 × 32 ≈ 18.4 桁 となって IEEE 754 の倍精度に到達できることになります。
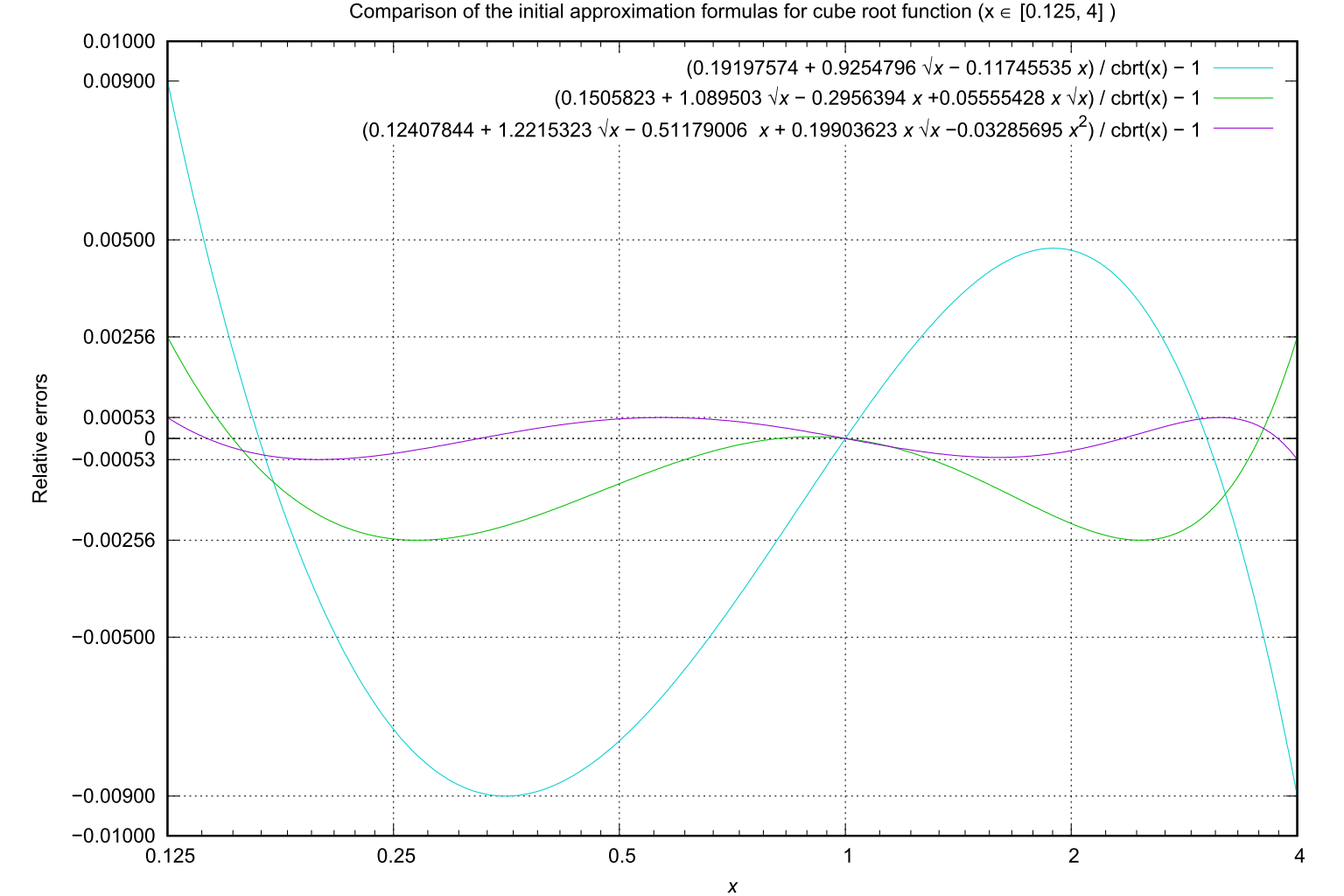
Fig.3: 立方根を平方根を含む 3〜5 項の級数で近似した場合の近似誤差 (x ∈ [0.125, 4])もし、式 (10) を x87 の 80-bit 拡張倍精度での計算に適用しようとすると、3次収束の漸化式 2回では拡張倍精度の 19 桁の精度には到達できません。その場合には次の [0.125, 4] の範囲において最適化した 4 項の初期近似式 (11) では、最大誤差が約 0.00256 すなわち約 2.59 桁の精度でしたので、同様に 2.59 × 32 = 23.3 桁 となって拡張倍精度に到達できることになります。
Listing 3:
_cbrt - cube root function in C89 (ANSI-C)#include <math.h> #include <float.h> double r_cbrt(double d); /* The _cbrt(d) function compute the cube root of d.*/ /* _rcbrt Rev.2.3 (May 13, 2025) (c) 2025 Takayuki HOSODA */ double r_cbrt(double d) { double r, x, a, c; int e; if (d == 0) return 0; r = frexp(fabs(d), &e); /* Range reduction: r is in [0.5, 1.0) */ x = ldexp(r, e % 3); /* x is in [0.125, 4) */ /* Initial approximation formula for x in [0.125, 4] with |err| < 0.00256 */ a = (0.1505823 - 0.2956394 * x) + (1.089503 + 0.0555543 * x) * sqrt(x); /* Apply the asymptotic formula of cubic convergence twice */ c = a * a * a; a += a * (x - c) / (c + c + x); c = a * a * a; a += a * (x - c) / (c + c + x); #ifndef OMIT_ADJ /* A 1-ulp correction to ensure result consistency. */ if (a * a * a * (1.0 - DBL_EPSILON) > x) a *= (1.0 - 0.5 * DBL_EPSILON); if (a * a * a * (1.0 + 2.0 * DBL_EPSILON) < x) a *= (1.0 + DBL_EPSILON); #endif return ldexp(d > 0.0 ? a : -a, e / 3); /* Return with range expansion */ }
Listing 4:
_cbrtl - cube root function in C89 (ANSI-C)#include <math.h> #include <float.h> long double r_cbrtl(long double d); /* The r_cbrtl(d) function compute the cube root of d.*/ /* r_cbrtl Rev.2.3 (May 13, 2025) (c) 2025 Takayuki HOSODA */ long double r_cbrtl(long double d) { long double r, x, a, c; int e; if (d == 0) return 0; r = frexpl(fabsl(d), &e); /* Range reduction: r is in [0.5, 1.0) */ x = ldexpl(r, e % 3); /* x is in [0.125, 4) */ /* Initial approximation formula for x in [0.125, 4] with |err| < 0.00256 */ a = (0.1505823 - 0.2956394 * x) + (1.089503 + 0.0555543 * x) * sqrtl(x); /* Apply the asymptotic formula of cubic convergence twice */ c = a * a * a; a += a * (x - c) / (c + c + x); c = a * a * a; a += a * (x - c) / (c + c + x); #ifndef OMIT_ADJ /* A 1-ulp correction to ensure result consistency. */ if (a * a * a * (1.0 - LDBL_EPSILON) > x) a *= (1.0 - 0.5 * LDBL_EPSILON); if (a * a * a * (1.0 + 2.0 * LDBL_EPSILON) < x) a *= (1.0 + LDBL_EPSILON); #endif return ldexpl(d > 0.0 ? a : -a, e / 3); /* Return with range expansion */ }注：
GCC 7.5 を用いた実験では、_cbrt および _cbrtl 関数に対して、1,000,000 個のランダムな倍精度・拡張倍精度の値を用いて評価を行いました。 相対誤差_cbrt(d)3 / d - 1および_cbrtl(d)3 / d - 1は、 それぞれ ±4.44089209850063e-16 および ±2.16840434497101e-19 以内に収まり、いずれも IEEE 754 におけるマシン・イプシロンの 2 倍以内でした。いずれの関数も負の引数に対応しており、
d < 0の場合には、それぞれ-_cbrt(-d), -_cbrtl(-d)を返します。 これは、立方根が奇数乗根であるため、実数全体で連続に定義できるという性質に基づいています。
実数立方根の実装例では、初期近似として平方根の項を含む近似式 (10) を用いました。 この近似式は以下の考えに基づいて設計されています。
x ≈ 1 付近における x2 の立方根の対して次数 (2, 0) の Padé 近似を行います。
その結果得られた式において x を √x で置き換えることで、 x 自身の立方根に対する近似式が得られます。
このとき、近似対象となる範囲も二乗されるため、立方根に対する近似誤差が少ない領域が拡がる効果が生じます。
得られた近似式をもとに、x = 1 で 1 になる条件を維持しつつ、x ∈ [0.125, 8] における近似誤差の絶対値が最小になるよう、 係数の最適化を行った例を Fig.4 に示します。
近似式 (10) は、C のfrexpとldexp関数とあわせて使うため、 同様に x ∈ [0.125, 4] において最適化したものです。
Fig.4: 立方根の二乗領域での近似 (x ∈ [0.125, 8])
参考として、同様の考えに基づいて設計した、より高次の近似式とその比較グラフを以下に示します。 これらは、平方根項を含む 4〜5 項程度の式によって x ∈ [0.125, 8] の範囲で立方根を近似した例です。
近似式 :
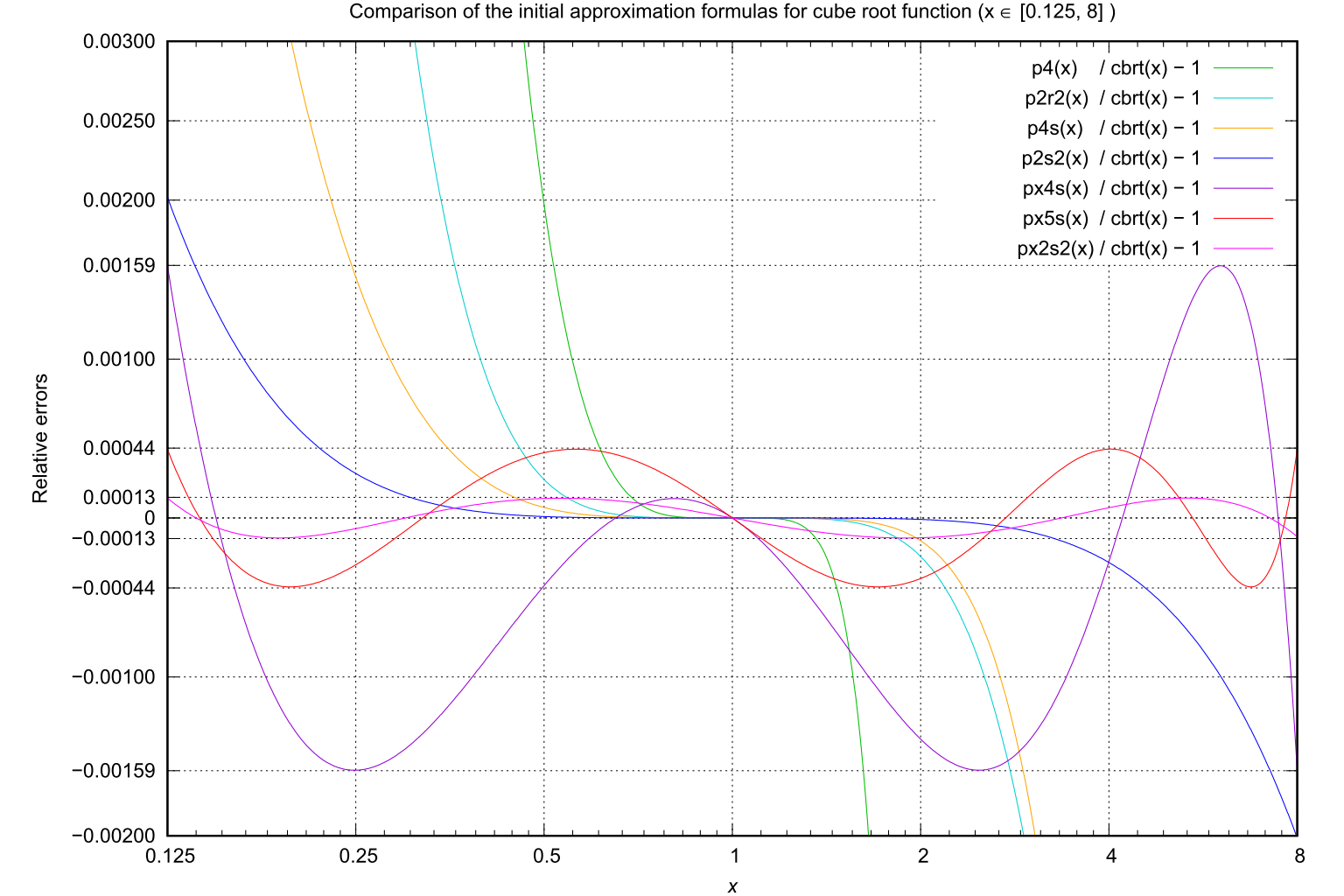
上記の手法をさらに拡張した例として、以下に高精度な初期近似の設計例を示します。
まず、立方根の (4, 4) Padé 近似式 (201) は、x ∈ [1/4√8, 4√8] の範囲において、
計算により 7.6 桁の以上の精度が示されています。
これに対し、3/4 乗根の Padé 近似をもとに構成した式 (202) では、
同程度の精度が x ∈ [0.125, 8] 、すなわち約 83/4 ≈ 4.76 倍に広がった範囲で得られます。
さらに、式 (202) をもとに係数の最適化を施した近似式 (203) では、同じ範囲で 9.0 桁>以上の精度が確認されました。
例えば、ややプリミティブな近似式である (105) と比較すると、除算と平方根演算がそれぞれ 1 回づつ増えるもの、
x ∈ [0.125, 8] において、約 7.2 桁（1.8 桁 → 9.0 桁）もの大幅な精度向上が確認されています（Fig.6 参照)。
このように、収束判定や条件分岐を必要とせず、またニュートン法などの反復計算を併用することなく、
初期近似のみで実用上十分な 9 桁以上の精度が得られる点は、計算時間の変動を嫌うリアルタイム制御などの産業応用において有用と考えられます。
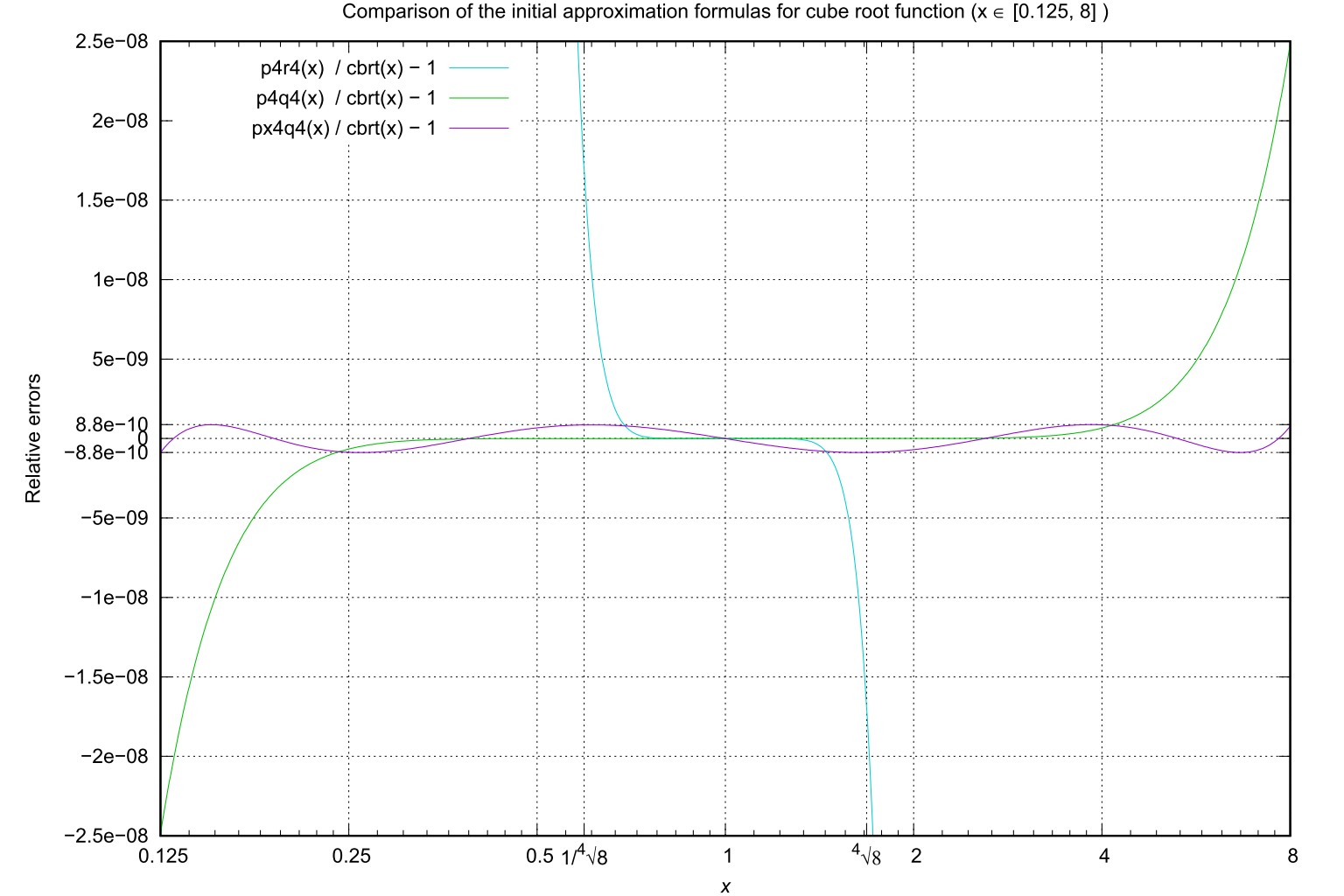
Fig.6: 立方根を４乗根を含む 8 項の展開式で近似した場合の近似誤差 (x ∈ [0.125, 8])
実用上の参考として、平方根を使わず、6 次の多項式による Min-Max 近似を初期値に用いた立方根関数の C プログラム例を以下に示します。
近似式 :
この近似式（式 (301)）では、x ∈ [0.5, 1] の範囲で 6.7 桁の精度が得られるため、 これを初期値として 1 回 Halley 法を適用すれば、理論上は 20.2 桁の精度に達し、 IEEE 754 の double（あるいは long double）形式の精度を満たします。
近似計算の後には、ULP レベルでの誤差補正を行っています。 複数のパイプラインや積和演算ユニットを持つプロセッサでは、前述の平方根を利用した_cbrt関数よりも、 本方式の方が高速に動作する可能性があります。
![\mathrm{pc6}(x) &=& \sum_{k=0}^6 c_k x^k, \quad x \in [0.5, 1] &(301)\\
\text{where:}
&& c_0 = 0.35489555,\ c_1 = 1.50819458,\\
&& c_2 = -2.11500172,\ c_3 = 2.44693876,\\
&& c_4 = -1.83469500,\ c_5 = 0.78493037,\\
&& c_6 = -0.14526271&\\
\mathrm{px4t}(x)&=& \sum_{k=0}^4 c_k x^{k/2}, \quad x \in [0.5, 1] &(302)\\
\text{where:}
&& c_1 = 0.1284692,\ c_2 = 1.21926614,\\
&& c_3 = -0.540296,\ c_4 = 0.2422709,\\
&& c_5 = -0.04971025\\
\mathrm{px5t}(x) &=& \sum_{k=0}^5 c_k x^{k/2}, \quad x \in [0.5, 1] &(303)\\
&& c_1 = 0.11132305,\ c_2 = 1.32115104,\\
&& c_3 = -0.78151144,\ c_4 = 0.52669338,\\
&& c_5 = -0.21674025,\ c_6 = 0.03908422\\](eqn-cbrt-c6.png)
Fig.7: 立方根の 6 次の多項式による Min-Max 近似の近似誤差 (x ∈ [0.5, 1])
Listing 5:
h_cbrt - cube root function in C89 (ANSI-C)#include <math.h> #include <float.h> double h_cbrt(double x); /* The h_cbrt(x) function compute the cube root of x. */ /* h_cbrt Rev.1.0 (May 7, 2025) (c) 2025 Takayuki HOSODA */ double h_cbrt(double x) { double a, b, c, d, t; int e; static const double scf[5] = { 0.62996052494743658238361, /* 1 / cbrt(4) */ 0.79370052598409973737585, /* 1 / cbrt(2) */ 1.0, 1.25992104989487316476721, /* cbrt(2) */ 1.58740105196819947475171 /* cbrt(4) */ }; if (x == 0) return 0; d = frexp(a = fabs(x), &e); /* d is in [0.5, 1) */ t = d * d; b = 0.78493037; c = - 0.14526271; b = b * t + 2.44693876; c = c * t - 1.83469500; b = b * t + 1.50819458; c = c * t - 2.11500172; b = b * d + 0.35489555; c = c * t + b; /* |error| < 1.715e-7 */ t = c * c * c; b = scf[2 + e % 3]; c = (c + c * (d - t) / (2 * t + d)) * ldexp(b, e / 3); if ((c * c * c) * (1 - DBL_EPSILON) > a) c *= (1 - 0.5 * DBL_EPSILON); if ((c * c * c) * (1 + 2 * DBL_EPSILON) < a) c *= (1 + DBL_EPSILON); return x > 0.0 ? c : -c; }
Listing 6:
h_cbrtl - cube root function in C89 (ANSI-C)long double ldexpl(long double x, int e); #include <math.h> #include <float.h> long double h_cbrtl(long double x); /* The h_cbrtl(x) function compute the cube root of x. */ /* h_cbrtl Rev.1.0 (May 8, 2025) (c) 2025 Takayuki HOSODA */ long double _cbrtl(long double x) { long double a, b, c, d, t; int e; static const long double scf[5] = { 0.62996052494743658238361L, /* 1 / cbrt(4) */ 0.79370052598409973737585L, /* 1 / cbrt(2) */ 1.0L, 1.25992104989487316476721L, /* cbrt(2) */ 1.58740105196819947475171L /* cbrt(4) */ }; if (x == 0) return 0; d = frexpl(a = fabsl(x), &e); /* d is in [0.5, 1) */ t = d * d; b = 0.78493037; c = - 0.14526271; b = b * t + 2.44693876; c = c * t - 1.83469500; b = b * t + 1.50819458; c = c * t - 2.11500172; b = b * d + 0.35489555; c = c * t + b; /* |error| < 1.715e-7 */ t = c * c * c; b = scf[2 + e % 3]; c = (c + c * (d - t) / (2 * t + d)) * ldexpl(b, e / 3); if ((c * c * c) * (1 - LDBL_EPSILON) > a) c *= (1 - 0.5 * LDBL_EPSILON); if ((c * c * c) * (1 + 2 * LDBL_EPSILON) < a) c *= (1 + LDBL_EPSILON); return x > 0.0 ? c : -c; }注：
GCC 7.5 を用いた実験では、h_cbrt および h_cbrtl 関数に対して、1,000,000 個のランダムな倍精度・拡張倍精度の値を用いて評価を行いました。 相対誤差h_cbrt(d)3 / d - 1およびh_cbrtl(d)3 / d - 1は、 それぞれ ±4.44089209850063e-16 および ±2.16840434497101e-19 以内に収まり、いずれも IEEE 754 におけるマシン・イプシロンの 2 倍以内でした。
先に示した平方根を使わない立方根関数は、
sqrtを使用していない点で軽量に見えますが、 初期近似に用いる多項式の項数が多く、定数のロードと積和演算（FMA）命令が多く発生するため、 処理性能の面での限界があります。 一方で、平方根を活用した初期近似は、適用範囲を x ∈ [0.5, 1] に限定することで、 より少ない項数で同等の精度が得られるため、特に高性能な浮動小数点ユニットを持つ処理系では高速に動作する可能性があります。たとえば、初期近似に 7 項の多項式を用いた式 (301) は約 6.8 桁の精度を持ちますが、平方根を利用する式 (302) では 5 項で約 6.7 桁の精度が得られています（Fig.7 参照）。
以下に、平方根を利用した初期近似による立方根関数の C プログラム例を示します。
Listing 7:
q_cbrt - cube root function in C89 (ANSI-C)#include <math.h> #include <float.h> double q_cbrt(double x); /* The q_cbrt(x) function compute the cube root of x. */ /* q_cbrt Rev.1.0 (May 9, 2025) (c) 2025 Takayuki HOSODA */ double q_cbrt(double x) { double a, b, c, d, t; int e; static const double scf[5] = { 0.62996052494743658238361, /* 1/cbrt(4) */ 0.79370052598409973737585, /* 1/cbrt(2) */ 1.0, 1.25992104989487316476721, /* cbrt(2) */ 1.58740105196819947475171 /* cbrt(4) */ }; if (x == 0) return 0; d = frexp(a = fabs(x), &e); /* d is in [0.5, 1] */ c = 0.12846922 - (0.54029596 + 0.0497103 * d) * d + (1.2192661 + 0.24227096 * d) * sqrt(d); /* |err| < 2.1e-7 */ b = scf[2 + e % 3]; t = c * c * c; c = (c + c * (d - t) / (2 * t + d)) * ldexp(b, e / 3); if ((c * c * c) * (1 - DBL_EPSILON) > a) c *= (1 - 0.5 * DBL_EPSILON); if ((c * c * c) * (1 + 2 * DBL_EPSILON) < a) c *= (1 + DBL_EPSILON); return x > 0.0 ? c : -c; }
Listing 8:
q_cbrtl - cube root function in C89 (ANSI-C)#include <math.h> #include <float.h> long double q_cbrtl(long double x); /* The q_cbrtl(x) function compute the cube root of x. */ /* q_cbrtl Rev.1.0 (May 9, 2025) (c) 2025 Takayuki HOSODA */ long double q_cbrtl(long double x) { long double a, b, c, d, t; int e; static const long double scf[5] = { 0.62996052494743658238361L, /* 1/cbrt(4) */ 0.79370052598409973737585L, /* 1/cbrt(2) */ 1.0, 1.25992104989487316476721L, /* cbrt(2) */ 1.58740105196819947475171L /* cbrt(4) */ }; if (x == 0) return 0; d = frexpl(a = fabsl(x), &e); /* d is in [0.5, 1] */ c = 0.12846922 - (0.54029596 + 0.0497103 * d) * d + (1.2192661 + 0.24227096 * d) * sqrtl(d); /* |err| < 2.1e-7 */ b = scf[2 + e % 3]; t = c * c * c; c = (c + c * (d - t) / (2 * t + d)) * ldexpl(b, e / 3); if ((c * c * c) * (1 - LDBL_EPSILON) > a) c *= (1 - 0.5 * LDBL_EPSILON); if ((c * c * c) * (1 + 2 * LDBL_EPSILON) < a) c *= (1 + LDBL_EPSILON); return x > 0.0 ? c : -c; }注：
GCC 7.5 を用いた実験では、q_cbrtおよびq_cbrtl関数に対して、1,000,000 個のランダムな倍精度・拡張倍精度の値を用いて評価を行いました。 相対誤差h_cbrt(d)3 / d - 1およびh_cbrtl(d)3 / d - 1は、 それぞれ ±4.44089209850063e-16 および ±2.16840434497101e-19 以内に収まり、いずれも IEEE 754 におけるマシン・イプシロンの 2 倍以内でした。
![x_0 &=& 0.191975 + 0.925482 \sqrt{a} - 0.117457 a, \quad \ x \in [0.125, 4]](eqn-cbrt-px3n.png){kind=small}
![x_0 &=& c_1 + c_2 a^{1/2} + c_3 a + c_4 a^{3/2}, \quad x \in [0.125, 4] &\\
\text{where:}&& c_1= 0.1505823,\quad c_2 = 1.089503,\\
&& c_3 = - 0.2956394,\ c_4 = 0.0555543](eqn-cbrt-px4n.png)
Function Under Test Relative error Execution time Note n=1000000 n=10000000 min max cputime [s] cbrt (Ref.#1) -5.55E-16 6.66E-16 0.187500 libm, system dependent __cbrt (Ref.#2) -1.55E-15 2.00E-15 0.250000 glibc-2.41, ieee754/dbl-64/s_cbrt.c q_cbrt -1.22E-15 6.66E-16 0.210938 OMIT_ADJ h_cbrt -1.22E-15 6.66E-16 0.218750 OMIT_ADJ r_cbrt -6.66e-16 6.66E-16 0.359375 OMIT_ADJ q_cbrt -4.44E-16 4.44E-16 0.242188 cf. Listing 7 h_cbrt -4.44E-16 4.44E-16 0.250000 cf. Listing 5 r_cbrt -4.44E-16 4.44E-16 0.437500 cf. Listing 3 cbrtl -3.25E-19 3.25-19 0.390625 80-bit long double, libm, system dependent q_cbrtl -2.17E-19 2.17E-19 0.414062 80-bit long double, cf. Listing 8 h_cbrtl -2.17E-19 2.17E-19 0.421875 80-bit long double, cf. Listing 6 r_cbrtl -2.17E-19 2.17E-19 0.648438 80-bit long double, cf. Listing 4 CPU: Intel(R) Xeon(R) CPU E3-1220 V2 @ 3.10GHz (3093.04-MHz K8-class CPU) CC: gcc7.5.0 -O2 -march=native
本稿では、平方根のみを用いて立方根を近似する手法と、その実装例について考察しました。 初期近似には、実数版では Puiseux 級数に類似した形に基づく近似式を、複素数版では x m/2n 型の指数近似用い、続いて Padé 型の反復法により精度の向上を図る構成を採りました。
提案する近似式および反復法は、比較的簡便な形でありながら、実数および複素数のいずれにおいても良好な収束性と精度を示すことが確認されました。 また、平方根の計算コストは除算と同程度であるため、本稿で紹介したアプローチは、広く一般的なものではないかもしれませんが、立方根計算における実用的な選択肢の一つになり得ると考えています。
今後、より高次の初期近似や他の反復法との比較検討により、さらに高精度または高速な手法が得られる可能性も期待されます。
※本稿で述べる、平方根を用いた立方根の初期近似に関する手法 — すなわち、 x 2/3 の Padé 近似を x = 1 近傍で構成し、 その後 x を √x に置き換えることで x 1/3 の関数に変換し、結果として有効な近似範囲を拡大するという方法 — は、 Puiseux 近似の着想に基づいて著者が独自に構成した手法であり、執筆時点においては同様の例を文献上に確認できておりません。
cbrt の使用法 (HP 42S)操作cbrt の計算例 (HP 42S)入力
出力
2 "cbrt" → 1.25992104989 -3 "cbrt" → 0.72112478515 + 1.24902476648 i 0 ENTER 1 COMPLEX "cbrt" → 0.866025403784 + 0.5 i 0 ENTER 10 COMPLEX "cbrt" → 1.86579517236 + 1.07721734502 i -16 ENTER 16 COMPLEX "cbrt" → 2 + 2 i 1e9 ENTER "cbrt" → 1000
![[Mail]](/~lyuka/images/mail.gif)
© 2000 Takayuki HOSODA.