円周率 π の計算には π/4 = arctan(1) に基づく各種の方法が多く使われていたが、 現在*Note1ではガウス (Johann Gauss 1777-1855) の算術幾何平均 (AGM, Arithmetic Geometric Mean) による 完全楕円積分 のアルゴリズムと、 楕円積分に関する ルジャンドル (Adrien-Marie Legendre 1752-1833) の関係式に基づく AGM アルゴリズムが主流になっている。
pi_gl — Program example using the Gauss–Legendre quadrature formula for π
very_long_float
pi_gl(iter)
int iter;
{
int i;
very_long_float a, b, t, x, y;
a = 1;
b = 1 / sqrt(2);
t = 1;
x = 4;
for (i = 0; i < iter; i++) {
y = a;
a = (a + b) / 2;
b = sqrt(y * b);
t -= x * sqr(y - a);
x *= 2;
}
return (sqr(a + b) / t);
}
sqr(x) は x2,
sqrt(x) は x1/2
この公式は2次の収束を示し、n 桁の答えが log2(n) 回程度の反復で求まる。
繰り返しごとの誤差は次のようになる。err( 1) = -3.2257622e-4 err( 2) = -2.3479336e-9 err( 3) = -5.8292283e-20 err( 4) = -1.7418264e-41 err( 5) = -7.6589246e-85 err( 6) = -7.3484406e-172 err( 7) = -3.3697129e-346 err( 8) = -3.5362794e-695 err( 9) = -1.9454428e-1393 err(10) = -2.9425892e-2790
pi_gl — Program example using P. Borwein's formula for the fourth-order convergence of π
very_long_float
pi_pb(iter)
int iter;
{
int i;
very_long_float a, b, y, t;
y = sqrt(2) - 1;
a = 6 - sqrt(32);
b = 8;
for (i = 0; i < iter; i++) {
t = qroot(1 - pow4(y));
y = (1 - t) / (1 + t);
t = sqr(1 + y);
a = sqr(t) * a - y * (t - y) * b;
b *= 4;
}
return (1 / a);
}
sqr(x) は x2,
pow4(x) は x4,
sqrt(x) は x1/2,
qroot(x) は x1/4)
この公式は4次の収束を示し、繰り返しごとの誤差は次のようになる。
err(1) = -2.3479336e-9 err(2) = -1.7418264e-41 err(3) = -7.3484406e-172 err(4) = -3.5362794e-695 err(5) = -2.9425892e-2790
pi_beeler — Beeler (1972) Recurrence Relation Formula for π
very_long_float h;
very_long_float a = 355.0/113.0; /* Initial approximation for pi */
while(abs(h = sin(a)) > epsilon) {
a += h;
}
この公式は 3 次の収束を示し、繰り返しごとの誤差は次のようになる。
err(1) = 1.007e-21 err(2) = 1.680e-63 err(3) = 7.804e-189
2002年12月6日 東京大学の金田 らによる π の世界新記録の更新 (1兆2400億桁) には分割有理数化法 (Divide and Rationalize methode) が使用された。
2009年8月の 筑波大学の 高橋大介 らによる π の世界記録の更新にも
ガウス・ルジャンドルのアルゴリズム と ボールウェインのアルゴリズムが使用された。
しかし 2009年12月の たった 1 台のデスクトップ PC を使った Fabrice Bellard による π の世界新記録の更新 (2兆6999億桁) には、 Ramanujan の π の無限級数の変種 Chudnovsky 兄弟 の式が使用された。
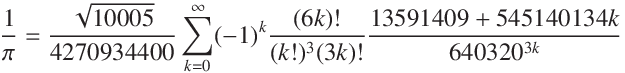
この公式の繰り返し毎の誤差は次のようになる。
err(0)= 1.8790e-14 err(1)= -9.7991e-29 err(2)= 5.4766e-43 err(3)= -3.1840e-57 err(4)= 1.8969e-71 err(5)= -1.1488e-85 err(6)= 7.0403e-100

![[Mail]](/~lyuka/images/mail.gif)



