１／ｆ雑音生成アルゴリズム

+Java Web Start １／ｆ雑音生成アルゴリズム

細田隆之
Feb. 1, 2002

１／ｆ雑音は増幅器の低周波域の雑音として有名なピンクノイズとも言われる３ｄＢ／オクターブで電力が減衰する雑音である。近年、１／ｆのゆらぎが人に心地よいとして、エアコンや扇風機の風量制御や照明などにも応用されている。そのような用途のために、疑似ホワイトノイズから１／ｆ雑音を生成するアルゴリズムを考案した。

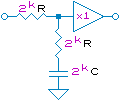
１／ｆの特性、つまり 3dB/oct. の特性を得るには様々な方法があろうが、ここでは、 fig.1 に示すラグリードフィルタ(lag-lead filter)を縦列接続したラダーフィルタ(ladder filter)に相当する伝達関数により１／ｆ特性を近似した。このラダーフィルタの伝達関数をデジタルフィルタで実現し、疑似ホワイトノイズにこのフィルターを施すことにより１／ｆ雑音を得ている。伝達関数 f(s) は次の式で表される。

Fig.1 ラグリードフィルタ伝達関数

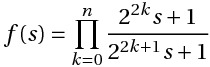$f(s)= \prod_{k=0}^n \displaystyle\frac{2^{2k}s+1}{2^{2k+1}s+1}$

(1) 式の周波数・振幅特性例を Fig.2 に示す。

Fig.2 近似式の振幅・周波数特性例 (k = -4～4) Fig.3 SPICE シミュレーション例

Download SPICE circuit netlist

下のＣプログラム例は、random() でホワイトノイズを生成した後に pinkfilter() で 3dB/oct のフィルタをかけている。 pinkfilter() は MAX_Z オクターブに渡って 3dB/oct の特性を示すデジタルフィルタをＩＩＲ型で構成している。 pinkfilter() を使用する前に、init_pink() を呼び出し、フィルタ係数を初期化する必要がある。


#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define MAX_Z 16

double  z[MAX_Z];
double  k[MAX_Z];

double pinkfilter(double in) {
    extern double   z[MAX_Z];
    extern double   k[MAX_Z];
    static double   t = 0.0;
    double          q;
    int             i;

    q = in;
    for (i = 0; i < MAX_Z; i++) {
        z[i] = (q * k[i] + z[i] * (1.0 - k[i]));
        q = (q + z[i]) * 0.5;
    }
    return (t = 0.75 * q + 0.25 * t); /* add 1st order LPF */
}

void init_pink() {
    extern double   z[MAX_Z];
    extern double   k[MAX_Z];
    int             i;

    for (i = 0; i < MAX_Z; i++)
        z[i] = 0;
    k[MAX_Z - 1] = 0.5;
    for (i = MAX_Z - 1; i > 0; i--)
        k[i - 1] = k[i] * 0.25;
}

int main() {
    int             i, j;
    double          n;

    init_pink();
    srandomdev();
    for (i = 0; i < 65536; i++) {
        printf("%.8g\n", pinkfilter(random() & 1 ? 1.0 : -1.0));
    }
}

Fig.4, Fig.5 にプログラム出力の波形とＦＦＴ結果の例を示す。

Fig.4 出力波形例 Fig.5 出力のＦＦＴ例 (2¹⁷ポイント Nuttall 窓^*note1)

Download PinkNoise Demo [5kB, Java Web Start]

⚠️ Demo の実行には Java 8 のインストールと例外サイトへの追加が必要です。

*note1: 窓関数

Fig.6 窓関数のDFT特性例

Blackman 窓 : 比較的狭帯域でメインローブ近傍のサイドローブが -68dB未満とまぁまぁでよく利用される。
　Blackman_Ex(x) = (7938 - 9240 cos(2πx) + 1430 cos(4πx)) / 18608 | 0 ≤ x ≤ 1

Nuttall(4b) 窓 : メインローブ近傍のサイドローブが約 -90dB と低く減衰率も -18dB/oct. と大きく汎用性が高い。
　 Nuttall_4b(x) = 2.355768 - 0.487396 cos(2πx) + 0.144232 cos(4πx) - 0.012604 cos(6πx) | 0 ≤ x ≤ 1

Blackman-Nuttall 窓 : メインローブ近傍からサイドローブが-98dB未満と割りと良く高ダイナミックレンジ向き。
　 Blackman-Nuttall(x) = 0.3635819 - 0.4891774 cos(2πx) + 0.1365995 cos(4πx) - 0.0106411 cos(6πx) | 0 ≤ x ≤ 1

Finetune5 窓 : デシメーション用に直流近傍のエイリアス周波数における減衰量を重視して設計したもの。

Fig.1 ラグリードフィルタ	伝達関数
	$f(s)= \prod_{k=0}^n \displaystyle\frac{2^{2k}s+1}{2^{2k+1}s+1}$

Fig.2 近似式の振幅・周波数特性例 (k = -4～4)	Fig.3 SPICE シミュレーション例

	Download SPICE circuit netlist

Fig.4 出力波形例	Fig.5 出力のＦＦＴ例 (2¹⁷ポイント Nuttall 窓^*note1)

Download PinkNoise Demo [5kB, Java Web Start]

SEE ALSO