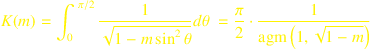
Dec. 27 2022
Takayuki HOSODA
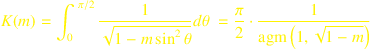

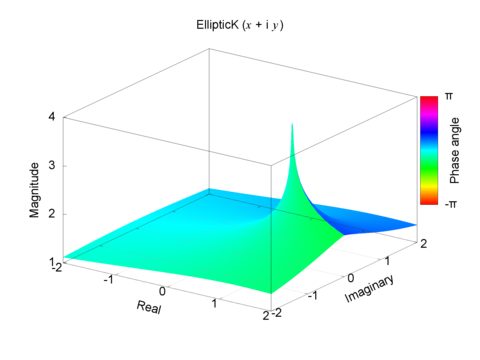
The calculation is performed using the relationship between Complete Elliptic Integrals of the First Kind and the Arithmetic Geometric Mean.
cEllipticK.c NAME _cEllipticK -- returns the complete elliptic integral of the first kind. LIBRARY Math library (libm, -lm)\n\ SYNOPSIS #include <math.h> #include <complex.h> #include <float.h> double complex _cEllipticK(double complex k); RETURN VALUE _cEllipticK(k) returns the complete elliptic integral of the first kind K(k)./* The complete elliptic integral of the first kind */ #include <math.h> #include <complex.h> #include <float.h> double complex _agm(double complex a, double complex b); double complex _cEllipticK(double complex); /** The arithmetic-geometric mean _agm(a, b) returns the arithmetic-geometric mean agm(a, b) of two numbers a and b. a_{n+1} &=& \frac{1}{2}(a_n + b_n)\\ b_{n+1} &=& \sqrt{a_n b_n} */ double complex _agm(double complex a, double complex b) { double e; double complex m; if ((cabs(a) == 0) || (cabs(b) == 0) || (a == -b)) return 0; e = 2.0 * DBL_EPSILON * fmax(cabs(a), cabs(b)); do { m = csqrt(a * b); a = (a + b) * 0.5; b = cabs(a + m) == cabs(a - m) ? cimag(m / a) > 0 ? -m : m : cabs(a + m) < cabs(a - m) ? -m : m; } while (cabs(a - b) > e); return (a + b) * 0.5; } /** The complete elliptic integral of the first kind _cEllipticK(m) returns the complete elliptic integral of the first kind K(m) The argument m is the parameter m = k^2, where k is the elliptic modulus. K(m) = \int_0^{\pi / 2} \frac{1}{ \sqrt{1 - m \sin^2 \theta }} d \theta */ double complex _cEllipticK(double complex m) { double complex c; c = csqrt(1.0 - m); if (cabs(c) == 0.0) return INFINITY; return M_PI_2 / _agm(1.0, c); } #ifdef DEBUG #include <stdio.h> #include <stdlib.h> char * help = "Name\n\ cEllipticK -- returns the complete elliptic integral of the first kind.\n\ Rev. 1.2 (Jan. 7, 2023) (c) 2022, Takayuki HOSODA (aka Lyuka)\n\ Usage\n\ cEllipticK m.re\n\ cEllipticK m.re m.im\n\ cEllipticK range_re range_im samples\n"; int main(int argc, char *argv[]) { double complex m; double complex c; double x, y; int n = 801; int r, j; if (argc == 2) { m = (atof(argv[1])); c = _cEllipticK(m); printf("_cEllipticK(%+g %+gi) = %+.16g %+.16gi\n", creal(m), cimag(m), creal(c), cimag(c)); }else if (argc == 3) { m = (atof(argv[1]) + I * atof(argv[2])); c = _cEllipticK(m); printf("_cEllipticK(%+g %+gi) = %+.16g %+.16gi\n", creal(m), cimag(m), creal(c), cimag(c)); } else if (argc == 4) { x = atof(argv[1]); y = atof(argv[2]); n = atof(argv[3]); if (n < 10) n = 10; printf("#Computed by \"_cEllipcK Rev.1.2 (Jan. 7, 2023) (c) 2022, Takayuki HOSODA (aka Lyuka)\n"); for (r = 0 ; r <= n; r++) { for (j = 0 ; j <= n; j++) { m = (-x * r + (n - r) * x) / n + I * ((-y * j + (n -j) * y) / n); c = _cEllipticK(m); printf("%.16g\t%.16g\t%.16g\t%.16g\n",creal(m), cimag(m), cabs(c), carg(c)); } printf("\n"); } } else { printf("%s\n", help); } return(0); } #endifDownload cEllipticK-1.21.tar.gz — The complete elliptic integral of the first kind. Rev.1.21 (Jan. 18, 2023) (c) 2022 Takayuki HOSODA
_cEllipticK(0) = 1.570796326794897 _cEllipticK(+0.09) = 1.608048619930513 _cEllipticK(+0.25) = 1.685750354812596 _cEllipticK(0.5) = 1.854074677301372 _cEllipticK(1) = inf + 0 i _cEllipticK(2) = 1.311028777146060 - 1.3110287771460600 i _cEllipticK(1 + i) = 1.509236954051273 + 0.6251464152026968 i _cEllipticK(-1 -i) = 1.265485522056594 - 0.1622369065268035 i
K(0) ~= 1.5707963267948966192313216916397514420985846996875529104874722961... K(0.09) ~= 1.6080486199305128012672072222386871571121767288026525584963492535... K(0.25) ~= 1.6857503548125960428712036577990769895008008941410890441199482978... K(0.5) ~= 1.8540746773013719184338503471952600462175988235217669055859280450... K(1) = complex infinity K(2) ~= 1.311028777146059905232419794945559706841377475715811581408410851... - 1.311028777146059905232419794945559706841377475715811581408410851... i K(1 + i) ~= 1.50923695405127282926831618488195455891391128404159452327369954... + 0.625146415202696884270118779602658813690462082446998873842351206... i K(-1 - i) ~= 1.26548552205659456855907495877407659312270799059591796880481132... - 0.162236906526803578322784600069554809100324122299479560182646882... i

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.