Algorithm for calculating π by Arithmetic-Geometric Mean
Various methods based on π/4 = arctan(1) were widely used to calculate π, but nowadays the algorithm for complete elliptic integration by arithmetic geometric mean of Gauss (Johann Gauss 1777-1855) and the arithmetic geometric mean algorithm based on the relation formula of LeJandre (Adrien-Marie Legendre 1752-1833) for elliptic integration have become mainstream.
*Note1
Example of a program using Gauss-Legendre's second-order convergence formula.
very_long_float
pi2(iter)
int iter;
{
int i;
very_long_float a, b, t, x, y;
a = 1;
b = 1 / sqrt(2);
t = 1;
x = 4;
for (i = 0; i < iter; i++) {
y = a;
a = (a + b) / 2;
b = sqrt(y * b);
t -= x * sqr(y - a);
x *= 2;
}
return (sqr(a + b) / t);
}
where sqr(x) is x2
The formula converges quadratically, and the n-digit answer can be obtained in about log2(n) iterations.
The error per iteration is as follows.
err( 1) = -3.2257622e-4
err( 2) = -2.3479336e-9
err( 3) = -5.8292283e-20
err( 4) = -1.7418264e-41
err( 5) = -7.6589246e-85
err( 6) = -7.3484406e-172
err( 7) = -3.3697129e-346
err( 8) = -3.5362794e-695
err( 9) = -1.9454428e-1393
err(10) = -2.9425892e-2790
Example of a program using P.Borwein's fourth-order convergence formula
very_long_float
pi(iter)
int iter;
{
int i;
very_long_float a, b, y, t;
y = sqrt(2) - 1;
a = 6 - sqrt(32);
b = 8;
for (i = 0; i < iter; i++) {
t = qroot(1 - pow4(y));
y = (1 - t) / (1 + t);
t = sqr(1 + y);
a = sqr(t) * a - y * (t - y) * b;
b *= 4;
}
return (1 / a);
}
where sqr(x) is x2, pow4(x) is x4, sqrt(x) is x1/2 and qroot(x) is x1/4.
This formula shows fourth-order convergence, and the error per iteration is as follows.
err(1) = -2.3479336e-9
err(2) = -1.7418264e-41
err(3) = -7.3484406e-172
err(4) = -3.5362794e-695
err(5) = -2.9425892e-2790
Extra. Beeler's formula like the Newton-Raphson method (1972).
very_long_float h;
very_long_float a0 = 355.0 / 113.0;
/* ai+1 = ai + sin(ai) converge to π.
* ai+1 = ai - tan(ai) does the same.
*/
while(abs(h = sin(a)) > epsilon) {
a += h;
}
This formula shows cubic convergence, and the error per iteration is as follows.
err(1) = 1.007e-21
err(2) = 1.680e-63
err(3) = 7.804e-189
Note1
As of September 1999. the Divide and Rationalize methode was used for the new world record of pi (1.24 trillion digits) set by Kanada et al. at the University of Tokyo on December 6, 2002. Gauss-LeJandre's algorithm and Ballwein's algorithm were also used to break the world record for pi by Daisuke Takahashi et al. of the University of Tsukuba in August 2009.
However, Ramanujan's infinite series variant of π, the Chudnovsky brothers' formula, was used for the new world record of π set by Fabrice Bellard in December 2009 (2.6999 trillion digits) using only one desktop PC.
Chudnovsky's formula
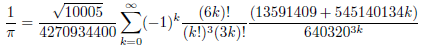
The error for each iteration of this formula is as follows.
err(0)= 1.8790e-14
err(1)= -9.7991e-29
err(2)= 5.4766e-43
err(3)= -3.1840e-57
err(4)= 1.8969e-71
err(5)= -1.1488e-85
err(6)= 7.0403e-100
SEE ALSO
REFERENCE
- J.Borwein and P.Borwein, Ramanujan and Pi, IEEE, Science and Applications, Supercomputing 88, Volume II, 117-128, 1988
- D.Takahashi, Y.Kanada, Improvement of the Algorithms for ƒÎ Calculation:The Gauss-Legendre Algorithm and the Borwein's Quartically Convergent Algorithm, IPSJ JOURNAL Abstract Vol.38 No.11 - 033
- Yasunori Ushiro, Yasumasa Kanada, Daisuke Takahashi, "A Divide and Rationalize MEthode which Improves the Multiple-precision Function Computation with Series Expansion", Transactions of Information Processing Society of Japan, Vol. 41 No. 6 pp. 1811-1819, June 2000
- David H. Bailey, Peter Borwein, and Simon Plouffe, On the rapid computaion of various polylogarithmic constants, Mathematics of Computation 66 (1997) 903-913.
External LINKS
5 Trillion Digits of Pi - New World Record(Aug. 7, 2010)
Numerical approximations of π - Wikipedia

![[Mail]](/~lyuka/images/mail.gif)

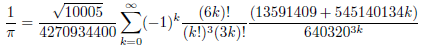

![[Mail]](/~lyuka/images/mail.gif)