M-series generator polynomials

Ｍ系列の生成多項式

Ch.1 : M-series, Ch.2 : Correration
細田隆之

デジタル通信分野で広く用いられているＭ系列(Maximum length sequence) と呼ばれる n ビットのシフトレジスタとフィードバックで生成される、周期が 2ⁿ - 1 の符号列がある。

回路構成

Ｍ系列生成回路は一般的にシフトレジスタに線形帰還をかけた LFSR (Linear Feedback Shift Register) で構成される。 LFSR はフィードバックの仕方で fig.1 に示す Fibonacci LFSR と fig.2 に示す Galois LFSR の２形式がある。各図中の (＋) 印は排他的論理和（eXclusive-OR）である。このシフトレジスタとフィードバックで形成している回路はつまり原始多項式での除算器であると言える。

$(9, 5)\ \;:& F_7(X) = X^9 + X^5 + 1 \qquad &|\; \mathrm{Fibonacci\ LFSR}$ output
fig.1 A Fibonacci model LFSR and its Generator Polynomial

$(9, 4)'\;:& G_7(X) = X^9 + X^4 + 1 \qquad &|\; \mathrm{Galois\ LFSR}$ output
fig.2 A Galois model LFSR and its Generator Polynomial

特徴と用途

応用的には、デジタル通信や計測のさまざまなところに使われていて、例えばフレーム同期信号やスクランブル、周波数拡散用の拡散符号や誤り率測定や測距や位置検出、擬似雑音発生などに利用されている。このように広く使われている訳は、Ｍ系列で生成されるビット列には、次のような特徴があるからである。

連続する 1 の長さは n 以下である

0 と 1 の発生個数が 1 周期で 1 だけ違う（0 と 1 の発生確率がほぼ同じ）

自己相関のピークが１周期に１度だけある。つまり、周期を N、ずれをτ として τ = k N (k = 0, 1, 2, …) の時 N で、それ以外のとき -1 である

n ビットのＭ系列の 1 周期の中の連続する n ビットはユニークである

1, 2 番めの特徴はＭ系列の１周期の平均値が 2^{n - 1} / (2ⁿ - 1) であるということであって、スクランブル等に利用されている。

3 番目の特徴はその１周期中に１度の大きな相関のため、雑音や誤りの影響があっても検知しやすく同期信号に多用されている。
また、周期を長く、つまり N を十分大きく取れば、ほとんどホワイトノイズに近似できるということでもある。(fig.4)

4 番目の特徴は、Ｍ系列中の n ビットから、ずれ τ が一意に決まるため、測距や絶対位置エンコーダーなどにも利用されている。

fig.3 自己相関の例 (n = 7)

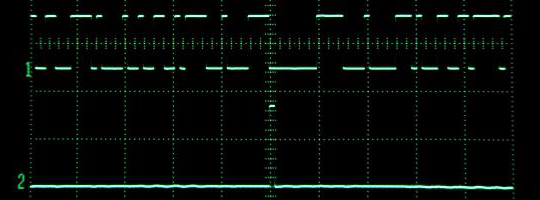
fig.4 実際の波形の例(n = 9, 7.3728 Mbps)
Ch1 : Pseudo-random pattern for systems using 2⁹ -1 pattern length
Ch2 : Correlation
Math: FFT (Hamming windowed)

生成多項式

下に筆者の知る範囲でまとめた主な生成多項式を示す。
簡便のため生成多項式は最下位の 1 を省き係数が 1 の次数のみを表記する。 e.g. X⁹ + X⁴ + 1 → (9, 4)
係数の上位～下位を入れ替えた生成多項式は互いに逆順の出力シーケンスとなるため、係数の小さい方のみを記載している。
但し、ITU-T の勧告では、この係数が大きい３項生成多項式を Fibonacci LFSR で用いているため、* 付きの太字で示してある。
e.g. 生成多項式 *(9,4) は (9,5) 即ち X⁹ + X⁵ + 1 を意味する。
次数
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32,
33, 35, 41, 47, 49, 52, 55, 57, 58, 61,
63, 65, 89, 127, 255, 521, 607, 756

2 : (2,1)
3 : (3,1)
4 : (4,1)
5 : (5,2), (5,4,3,2), (5,4,2,1)
6 : (6,1), (6,5,2,1), (6,5,3,2)
7 : *(7,1), (7,3), (7,3,2,1), (7,4,3,2), (7,6,4,2), (7,6,3,1), (7,6,5,2), (7,6,5,4,2,1), (7,5,4,3,2,1)
8 : (8,4,3,2), (8,6,5,3), (8,6,5,2), (8,5,3,1), (8,6,5,1), (8,7,6,1), (8,7,6,5,2,1), (8,6,4,3,2,1)
9 : *(9,4), (9,6,4,3), (9,8,5,4), (9,8,4,1), (9,5,3,2), (9,8,6,5), (9,8,7,2), (9,6,5,4,2,1), (9,7,6,4,3,1), (9,8,7,6,5,3)
10 : (10,3), (10,8,3,2), (10,4,3,1), (10,8,5,1), (10,8,5,4), (10,9,4,1), (10,8,4,3), (10,5,3,2), (10,5,2,1), (10,9,4,2)
11 : *(11,2), (11,8,5,2), (11,7,3,2), (11,5,3,2), (11,10,3,2), (11,10,3,2), (11,6,5,1), (11,5,3,1), (11,9,4,1), (11,8,6,2), (11,9,8,3)
12 : (12,6,4,1), (12,9,3,2), (12,11,10,5,2,1), (12,11,6,4,2,1), (12,11,9,7,6,5), (12,11,9,5,3,1), (12,11,9,8,7,4), (12,11,9,7,6,5), (12,9,8,3,2,1), (12,10,9,8,6,2)
13 : (13,4,3,1), (13,10,9,7,5,4), (13,11,8,7,4,1), (13,12,8,7,6,5), (13,9,8,7,5,1), (13,12,6,5,4,3), (13,12,11,9,5,3), (13,12,11,5,2,1), (13,12,9,8,4,2), (13,8,7,4,3,2)
14 : (14,12,2,1), (14,13,4,2), (14,13,11,9), (14,10,6,1), (14,11,6,1), (14,12,11,1), (14,6,4,2), (14,11,9,6,5,2), (14,13,6,5,3,1), (14,13,12,8,4,1), (14,8,7,6,4,2), (14,10,6,5,4,1), (14,13,12,7,6,3), (14,13,11,10,8,3)
15 : *(15,1), (15,13,10,9), (15,13,10,1), (15,14,9,2), (15,9,4,1), (15,12,3,1), (15,10,5,4), (15,10,5,4,3,2), (15,11,7,6,2,1), (15,7,6,3,2,1), (15,10,9,8,5,3), (15,12,5,4,3,2), (15,10,9,7,5,3), (15,13,12,10), (15,13,10,2), (15,12,9,1), (15,14,12,2), (15,13,7,4,1), (15,4), (15,13,7,4)
16 : (16,12,3,1), (16,12,9,6), (16,9,4,3), (16,12,7,2), (16,10,7,6), (16,15,7,2), (16,9,5,2), (16,13,9,6), (16,15,4,2), (16,15,9,4)
17 : (17,3), (17,3,2,1), (17,7,4,3), (17,16,3,1), (17,12,6,3,2,1), (17,8,7,6,4,3), (17,11,8,6,3,2), (17,9,8,6,4,1), (17,16,14,10,3,2), (17,12,11,8,5,2)
18 : (18,7), (18,10,7,5), (18,13,11,9,8,7,6,3), (18,17,16,15,10,9,8,7), (18,15,12,11,9,8,7,6)
19 : (19,5,2,1), (19,13,8,5,4,3), (19,12,10,9,7,3), (19,17,15,14,13,12,6,1), (19,17,15,14,13,9,8,4,2,1), (19,16,13,11,10,9,4,1), (19,9,8,7,6,3), (19,16,15,13,12,9,5,4,2,1), (19,18,15,14,11,10,8,5,3,2), (19,18,17,16,12,7,6,5,3,1)
20 : *(20,3), (20,9,5,3), (20,19,4,3), (20,11,8,6,3,2), (20,17,14,10,7,4,3,2)
21 : (21,2), (21,14,7,2), (21,13,5,2), (21,14,7,6,3,2), (21,8,7,4,3,2), (21,10,6,4,3,2), (21,15,10,9,5,4,3,2), (21,14,12,7,6,4,3,2), (21,20,19,18,5,4,3,2)
22 : (22,1), (22,9,5,1), (22,20,18,16,6,4,2,1), (22,19,16,13,10,7,4,1), (22,17,9,7,2,1), (22,17,13,12,8,7,2,1), (22,14,13,12,7,3,2,1)
23 : *(23,5), (23,17,11,5), (23,5,4,1), (23,12,5,4), (23,21,7,5), (23,16,13,6,5,3), (23,11,10,7,6,5), (23,15,10,9,7,5,4,3), (23,17,11,9,8,5,4,1), (23,18,16,13,11,8,5,2)
24 : (24,7,2), (24,4,3,1), (24,22,20,18,16,14,11,9,8,7,5,4), (24,21,19,18,17,16,15,14,13,10,9,5,4,1)
25 : (25,3), (25,3,21), (25,20,5,3), (25,12,4,3), (25,17,10,3,2,1), (25,23,21,19,9,7,5,3), (25,18,12,11,6,5,4), (25,20,16,11,5,3,2,1), (25,12,11,8,7,6,4,3)
26 : (26,6,2,1), (26,22,21,16,12,11,10,8,5,4,3,1)
27 : (27,5,2,1), (27,18,11,10,9,5,4,3)
28 : (28,3), (28,13,11,9,5,3), (28,22,11,10,4,3), (28,24,20,16,12,8,4,3,2,1)
29 : (29,2), (29,20,11,2), (29,13,7,2), (29,21,5,2), (29,26,5,2), (29,19,16,6,3,2), (29,18,14,6,3,2)
30 : (30,23,2,1), (30,6,4,1), (30,24,20,16,14,13,11,7,2,1)
31 : (31,29,21,17), (31,28,19,15), (31,3), (31,3,2,1), (31,13,8,3), (31,30,29,25), (31,28,24,10), (31,20,15,5,4,3), (31,16,8,4,3,2)
32 : (32,22,2,1), (32,7,5,3,2,1), (32,28,19,18,16,14,11,10,9,6,5,1)
33 : (33,13), (33,22,13,11), (33,26,14,10), (33,6,4,1), (33,22,16,13,11,8)
35 : (35,2)
39 : (39,4), (39,8), (39,14)
41 : (41,3), (41,20)
47 : (47,5), (47,14), (47,20)
49 : (49,9), (49,12), (49,15), (49,22)
52 : (52,19)
55 : (55,24)
57 : (57,7), (57,22)
58 : (58,19)
59 : (59,58,38,37)
60 : (60,59)
61 : (61,5,2,1)
62 : (62,61,6,5)
63 : (63,1), (63,5), (63,31)
64 : (64,63,61,60)
65 : (65,18), (65,32)
89 : (89,51), (89,6,5,3)
93 : (93,91)
94 : (94,73)
95 : (95,84)
97 : (97,91)
98 : (98,87)
100 : (100,63)
127 : (127,1), (127,7), (127,15), (127,30), (127,63)
255 : (255,52), (255,56), (255,82)
521 : (521,32), (521,48), (521,158)
524 : (524,167)
607 : (607,105), (607,147), (607,273)
756 : (756,19)

REFFERENCES

W. P. Horton, "Shift Counters," Computer Control Corporation.
W. W. Peterson, "Error Correctiong Codes," MIT Press, Wiley, New York.
R. C. White, Jr., "Experiments with Digital Computer Simulation of Pseudo-Random Noise Gerenatiors, " IEEE Trans. Elect. Comp., June 1967.
M. Goresky and A. M. Klapper, "Fibonacci and Galois representations of feedback-with-carry shift registers," in IEEE Transactions on Information Theory, vol. 48, no. 11, pp. 2826-2836, Nov. 2002, doi: 10.1109/TIT.2002.804048.
ITU-T O.151
ITU-T O.153

履歴

1993年7月2日初版
2012年2月10日改訂
2024年6月26日改訂

回路構成

特徴と用途

生成多項式

REFFERENCES

履歴

関連項目