
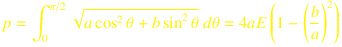
E(m) is the complete elliptic integral of the second kind with parameter m = k2
2023年 1月18日
細田 隆之

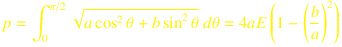
 English edition is here.
English edition is here.第二種完全楕円積分を用いて計算しています。
ラマヌジャンの楕円の周長の近似値も計算しています。
Download perimeter-0.2.js— source codeより正確な値の例(WolframAlpha による) a = 1, b = 1 : 6.2831853071795864769252867665590057683943387987502116419498891846... = 2π (厳密に) a = 2, b = 1 : 9.6884482205476761984285031963918294119539183978866008250831163524... a = 5, b = 1 : 21.010044539689000944699164588473738912894812339134152623096835657... a = 10, b = 1 : 40.639741801008957425577931011816563791313052134504059403405927819...

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.