Online calculator
Analysis of the Conductor-backed edge coupled coplanar waveguide



Takayuki HOSODA
Dec. 26, 2022

Conductor-backed edge coupled coplanar waveguide calculator

In this calculation, the ground planes are assumed to be wider than 6h + 2g + s + 2w and the conductor thickness is thinner than 0.35 w, and the upper conductor plane, if exists, is located higher than 15 (h + t).

Frequency    MHz
Electrical length    deg
Dielectric relative permittivity (εr )   
Dielectric height (h )   μm
Signal line width (w)     μm
Signal line separation (s)     μm
Distance to side grounds(d)     μm
Conductor thickness (t)    μm
Differential impedance (Zdiff = 2 * Z0, o) ≈    Ω
Odd mode impedance (Z0, o) ≈    Ω
Even mode impedance (Z0, e) ≈    Ω
Odd mode effective permittivity (Εeff, o) ≈    
Even mode effective permittivity (Εeff, e) ≈    
Crosstalk Coefficient (ξ) ≈     
Velocity of propagation (v) ≈     
Phisical length ≈ (ℓ)     mm
z_edge_coupled_cbcpw-0.8.js — Analyze Edge-coupled Conductor-backed Coplanar Waveguide. Rev. 0.8 (Jan. 26, 2023) (c) Takayuki HOSODA.

Formulas used [1], [3]

Z_\mathrm{0,o} &=& \frac{\eta_0}{ \sqrt{\varepsilon_\mathrm{eff,o}}} \left(\frac{1}{2\displaystyle \frac{K(k_\mathrm{o})}{K'(k_\mathrm{o})} +\frac{K( \beta_1)}{K'(\beta_1)}}\right)\\ \\ Z_\mathrm{0,e} &=& \frac{\eta_0}{ \sqrt{\varepsilon_\mathrm{eff,e}}} \left(\frac{1}{2\displaystyle \frac{K(k_\mathrm{e})}{K'(k_\mathrm{e})} +\frac{K( \beta_1 k_1)}{K'(\beta_1 k_1)}}\right)
\varepsilon_\mathrm{eff,o} &=& \frac{2 \varepsilon_r \displaystyle \frac{K(k_\mathrm{o})}{K'(k_\mathrm{o})}+\frac{K( \beta_1 )}{K'(\beta_1)}} {2\displaystyle \frac{K(k_\mathrm{o})}{K'(k_\mathrm{o})}+\frac{K( \beta_1)}{K'(\beta_1)}}\\ \\ \varepsilon_\mathrm{eff,e} &=& \frac{2 \varepsilon_r \displaystyle \frac{K(k_\mathrm{e})}{K'(k_\mathrm{e})}+\frac{K( \beta_1 k_1)}{K'(\beta_1 k_1)}} {2\displaystyle \frac{K(k_\mathrm{e})}{K'(k_\mathrm{e})}+\frac{K( \beta_1 k_1)}{K'(\beta_1 k_1)}}
K'(k) = K\left(\sqrt{1 - k^2}\right)
\beta_1 &=& \sqrt{\frac{1 - y^2}{1 - k_1^2 \, y^2}}\\ k_1 &=& \frac{s + 2w}{s + 2w + 2d}\\ y &=& \frac{s}{s + 2w}
k_\mathrm{o} &=& \lambda \frac {- \sqrt{\lambda^2 - t_\mathrm{C}^2} + \sqrt{\lambda^2 - t_\mathrm{B}^2} } {t_\mathrm{B} \sqrt{\lambda^2 - t_\mathrm{C}^2} + t_\mathrm{C} \sqrt{\lambda^2 - t_\mathrm{B}^2}}\\ \lambda &=& \frac{1}{2} \sinh^2\left(\frac{\ \pi }{2h}\left(\frac{s}{2} + w + d \right)\right)\\ t_\mathrm{C} &=& \sinh^2\left(\frac{\pi }{2h}\left(\frac{s}{2} + w \right)\right) - \lambda\\ t_\mathrm{B} &=& \sinh^2\left(\frac{\pi s}{4h}\right) - \lambda
k_\mathrm{e} &=& \lambda' \frac {- \sqrt{\lambda'^2 - t'_\mathrm{C}^2} + \sqrt{\lambda'^2 - t'_\mathrm{B}^2} } {t'_\mathrm{B} \sqrt{\lambda'^2 - t'_\mathrm{C}^2} + t'_\mathrm{C} \sqrt{\lambda'^2 - t'_\mathrm{B}^2}}\\ \lambda' &=& \frac{1}{2} \cosh^2\left(\frac{\ \pi }{2h}\left(\frac{s}{2} + w + d \right)\right)\\ t'_\mathrm{C} &=& \sinh^2\left(\frac{\pi }{2h}\left(\frac{s}{2} + w \right)\right) - \lambda' + 1\\ t'_\mathrm{B} &=& \sinh^2\left(\frac{\pi s}{4h}\right) - \lambda' + 1
\xi &=& \frac{Z_\mathrm{o,e} - Z_\mathrm{0,o} }{Z_\mathrm{o,e} + Z_\mathrm{0,o}}

Conductor thickness compensation

The above analytical solution by Hanna (1985) is for negligibly thin conductor thicknesses, but the thickness of conductors used in real circuit boards has a non-negligible effect. As I am unaware of any formula that includes conductor thickness, I will use the following formula to compensate for the case where conductor thickness t < 0.35w, 0.35s, 0.35d and the dielectric relative permittivity 2.2 < ϵr < 10.2. This correction value of δ is not an analytical value, but an approximate correction based on electromagnetic field simulations in the practical range, so it may not be accurate enough in some cases. However, as far as I have confirmed, it seems to be within ± 4 % of the impedance calculated by electromagnetic field simulation. Without this correction, the error is more pronunced for large t / w, low relative permittivity and small gap. e.g. t / w = 0.35, er = 2.2, s / w = 1, d / w = 1.5, the error is about 25 %. The other simplest correction formula would be δ = t, which yields a maximum error of 7 % when calculated under the same conditions.
Note: This formula is subject to change without notice due to experimental results for improvement.

\delta &=& \displaystyle\frac{8.82 \ t\left(1 + \displaystyle\frac{1}{\varepsilon_{\mathrm{r}}}\right)}{1 + \sqrt{ \displaystyle\frac{1396 \ t}{0.457\ (w + d) + s + t}}}\\ w & \leftarrow & w + \delta \\ s & \leftarrow & s - \delta \\ d & \leftarrow & d - \delta

REFERENCE

APPENDIX 1

Examples of electromagnetic field simulations results (ground plane width b=3200, upper conductor height g=3200) Length unit in [ μm ]. 

w=340, s=200, d=400, h=400, t=35, ϵr=4.7 : Zodd=50.031 Ω, Zeven=83.260 Ω → Zdiff=100.062 Ω
w=310, s=200, d=200, h=200, t=18, ϵr=4.6 : Zodd=44.992 Ω, Zeven=58.004 Ω → Zdiff= 89.984 Ω
w=240, s=190, d=200, h=200, t=18, ϵr=4.6 : Zodd=50.380 Ω, Zeven=67.018 Ω → Zdiff=100.760 Ω
Pseudo color visualization of absolute value of electric field in odd mode
Pseudo color visualization of absolute value of the electric field in odd mode.

APPENDIX 2

The ratio of the complete elliptic integrals of the first kind K(k) and K(k') can be calculated by the following relation with the ratio of arithmetic-geometric means. The argument k is the elliptic modulus.
\frac{K(k)}{K(k')} & = & \displaystyle\frac{\mathrm{agm}(1, k)}{\mathrm{agm}(1, k')}\\ \\ k' &=& \sqrt{1 - k^2}
where agm(1, k) is the arithmetic-geometric mean of 1 and k.

SEE ALSO

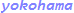
www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.