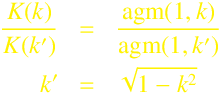
Dec. 17 2022
Takayuki HOSODA
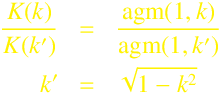

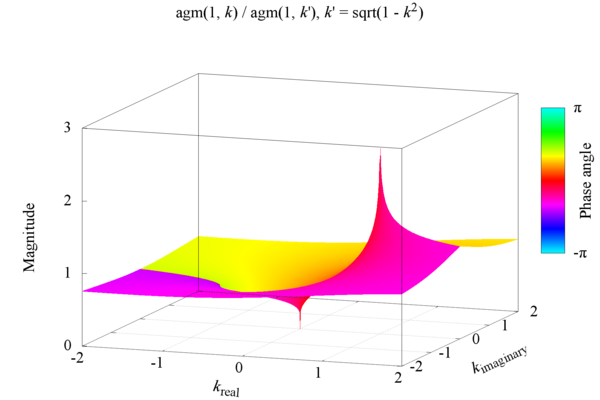
The ratio of the complete elliptic integral of the first kind appears, for example, in formulas for coplanar transmission lines, which are often used in the transmission of microwave or high-speed digital signals. Before the emergence of digital computers, the Approximation Formula by W. Hilberg was widely used to calculate it. Nowadays, a 3D plot of the accurate ratio of complex complete elliptic integral of first kind, as shown in the cover image, can be produced in a second.
cEllipticK.c NAME _cEllipticKRatio -- returns the ratio of the complete elliptic integral of the first kind K(k)/K(k'). LIBRARY Math library (libm, -lm)\n\ SYNOPSIS #include <math.h> #include <complex.h> #include <float.h> double complex _cEllipticKRatio(double complex k); RETURN VALUE _cEllipticKRatio(k) returns the ratio of the complete elliptic integral of the first kind K(k)/K(k'). The argument k is the elliptic modulus.
Exact formulaEquation for the ratio of the complete elliptic integral of the first kind and the ratio of the arithmetic-geometric mean.
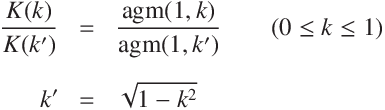
where, k is the elliptic modulus.
/* The ratio of the complete elliptic integrals of the first kind K(k) and K(k'). */ #include <math.h> #include <complex.h> #include <float.h> double complex _cEllipticKRatio(double complex k); double complex _agm(double complex a, double complex b); /** The arithmetic-geometric mean _agm(a, b) returns the arithmetic-geometric mean agm(a, b) of two numbers a and b. a_{n+1} &=& \frac{1}{2}(a_n + b_n)\\ b_{n+1} &=& \sqrt{a_n b_n} */ double complex _agm(a, b) double complex a; double complex b; { double e; double complex m; if ((cabs(a) == 0) || (cabs(b) == 0) || (a == -b)) return 0; e = 2 * DBL_EPSILON * fmax(cabs(a), cabs(b)); do { m = csqrt(a * b); a = (a + b) * 0.5; b = ((cabs(a + m) == cabs(a - m)) && (cimag(m / a) > 0)) || (cabs(a + m) < cabs(a - m)) ? -m : m; } while (cabs(a - b) > e); return ((a + b) * 0.5 ); } /** The ratio of the complete elliptic integrals of the first kind K(k) and K(k'). * The argument k is the elliptic modulus. * It can be calculated by the following relation with the ratio of the arithmetic-geometric means. \frac{K(k)}{K(k')} & = & \displaystyle\frac{\mathrm{agm}(1, k)}{\mathrm{agm}(1, k')}\\ k' &=& \sqrt{1 - k^2} */ double complex _cEllipticKRatio(k) double complex k; { return _agm(1, k) / _agm(1, csqrt(1 - k * k)); } #ifdef DEBUG #include <stdio.h> #include <stdlib.h> char * help = "Name\n\ cEllipticKRatio -- returns the ratio of the complete elliptic integrals of the first kind K(k) and K(k').\n\ The argument k is the elliptic modulus.\n\ Rev. 1.2 (Jan. 9, 2023) (c) 2023, Takayuki HOSODA, Finetune co., ltd.\n\ Usage\n\ cEllipticKRatio k.re k.im\n\ Example\n\ cEllipticKRatio(0.3) = 0.611943427652876\n\ cEllipticKRatio(0.5) = 0.7817009613480558\n\ "; int main(int argc, char *argv[]) { double complex k; double complex c; double d; int n = 800; int r, j; if (argc == 3) { k = (atof(argv[1]) + I * atof(argv[2])); c = _cEllipticKRatio(k); printf("cEllipticKRatio(%+g %+gi) = %+.16g %+.16gi\n", creal(k), cimag(k), creal(c), cimag(c)); } else if (argc == 2) { d = atof(argv[1]); printf("#Computed by \"cEllipcRatio Rev.1.2 (Jan. 9, 2023) (c) 2022, Takayuki HOSODA\n"); printf("#z.re\tz.im\tmagnitude\tphase angle\n"); for (r = 0 ; r <= n; r++) { for (j = 0 ; j <= n; j++) { k = (-d * r + (n - r) * d) / n + I * ((-d * j + (n -j) * d) / n); c = _cEllipticKRatio(k); printf("%.16g\t%.16g\t%.16g\t%.16g\n",creal(k), cimag(k), cabs(c), carg(c)); } printf("\n"); } } else { printf("%s\n", help); } return(0); } #endifDownload cEllipticKRatio-1.2.tar.gz — The ratio of the complete elliptic integral of the first kind. Rev.1.2 (Jan. 18, 2023) (c) 2022 Takayuki HOSODA
W. Hilberg's approximation for the ratio of the complete elliptic integrals K(k) / K(k').
Approximation errors
The Hilberg approximation appears to be good enough with an accuracy of 8-digits for k in the range of 0.02 < k < 0.998 and 4×10-12 for 0.125 < k < 0.99.
However, direct calculation of the ratio of elliptic integrals of the first kind by using the relation to the ratio of the arithmetic-geometric mean shown below on a personal computer yields highly accurate results with more than twice as fast as the approximate calculation.
Download ellipticKratio.js (javascript) — The ratio of the complete elliptic integral of the first kind. Rev.1.2 (Feb. 26, 2023) (c) 2022 Takayuki HOSODA
Reference values of K(k) / K(k') where, k is the elliptic modulus and k' = √(1 - k2)# k K(k) / K(k') 0.000001 0.10332959376573524262567981889968813952781247628389 0.00001 0.12177452186843340795096951738999918920646803727721 0.001 0.18938834975705311079390863822540396213248893750328 0.01 0.26217344174312708224926569320073820678498800737150 0.1 0.42610933023021026506647432449694583749832542276265 0.2 0.52613019289297166927435227689959465387833172017238 0.3 0.61194342765287608218700508871642169534903259182196 0.4 0.69513211551380288182549366132106909830794307581281 0.5 0.78170096134805575347524406433892877683776333817271 0.6 0.87743766134822250568861952396138288890348677788401 0.7 0.99090173267073761323809474605521423024825234999830 sqrt(0.5) 1 0.8 1.13968210398383736809112222988801592727980663647894 0.9 1.37829455195653131762704955576713917039417054189298 0.99 2.12618044709748639274810783574562976462874398715862 0.999 2.86055438243686323732070592454991597354628238086486 0.9999 3.59363327988449235808087504673903556513469596365228 0.99999 4.32658320329969422207650370981574290569904011134139 0.999999 5.05952023457951845039394133142912729741136838928772

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.