Forward voltage of a diode connected to Vin through a resistor


Vf calculator

Vin : Input voltage    [V]
R : Series resistance    [Ω]
Tj : Junction temperature    [°C]
Diode model 

TNOM : Nominal temperature     [°C]
Is(TNOM) : Saturation current    [A]
n : Emission coefficient   
Eg : Energy gap    [eV]
XTI : Is temperature exponent   
Rs : Ohmic resistance   
Vf : Forward voltage ≈     [V]
If : Forward current ≈     [mA]

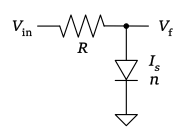
Note:
The calculation model used here does not take into account the backward diode components.
In the high current range exceeding several tens of mA, the results may differ significantly from the calculations.

Formulas used

Eg : energy gap 1.11 [eV]
k : Boltzmann constant 1.380649 × 10-23 [J K-1]
q : elementary charge 1.602176634 × 10-19 [C]
n : emission coefficient
T0 : Nominal temperature in Kelvin. 273.15 + 27 [K]
T1 : Junction temperature in Kelvin. 273.15 + Tj [K]
XTI : Saturation current temperature exponent. Usually equal to 3 for junction diodes, 2 for Schottky barrier diodes.

I_{s} = I_{s(T_0)}\left(\frac{T_1}{T_0}\right)^{\displaystyle\frac{X_{TI}}{n}}\exp\left(\frac{E_g q T_1 T_0}{n k (T_1 - T_0)}\right)

V_T = \frac{k T}{q}
V_\mathrm{f} &=& I_s R + V_\mathrm{in} - n V_T W_0\left( \frac{I_s R}{n V_T} \exp\left(\frac{I_s R + V_\mathrm{in}}{n V_T}\right)\right)

For high Vin, such as Vin > 220 n VT, the following Newton-Raphson method is used.

f(V_f}) &=& \exp\left(\frac{V_f}{n V_T}\right) - 1 - \frac{V_\mathrm{in} - V_f}{I_s R}\\ f'(V_f}) &=& \frac{V_f}{n V_T}\exp\left(\frac{V_f}{n V_T}\right) + \frac{V_f}{I_s R}\\ {V_f}_\mathrm{n+1} &\leftarrow& {V_f}_\mathrm{n} - \frac{f'(x)}{f(x)}

Appendix

fig.1 Example of a plot of calculation results

fig.2 Example of Vf characteristics of a real diode (Adapted from Nexperia, BAV70 datasheet)
Forward current as a function of forward voltage; typcal values

Reference

See also

www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.