サイン波の周波数スイープについて

in C89
サイン波の周波数スイープについて

#gnuplot 6.0
reset
unset xtics
unset ytics
set object 2 rect from graph 0, graph 0 to graph 1, graph 1 behind
set object 2 rect fc rgb

#gnuplot 6.0
reset
unset xtics
unset ytics
set object 2 rect from graph 0, graph 0 to graph 1, graph 1 behind
set object 2 rect fc rgb

2012 年 10月 10日
2025 年 5月 26日改定
細田隆之
English

English edition is here.

始めに

一定周波数のサイン波は通常は次のように書かれます:

$x(t) &=& \sin(2\pi f t)$
ここで: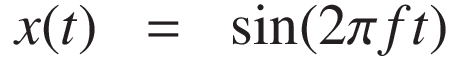

f は周波数 [Hz]
t は時間 [秒]
2πft 角周波数 [rad]

周波数が時間とともに変わる周波数スイープと呼ばれる場合には次のようになります:

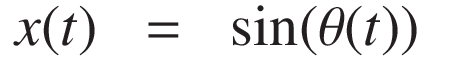
$x(t) &=& \sin(\theta(t))$

ここでθ(t) 時刻 t における角度（位相）で、それは瞬時周波数 f(t) を積分することにより得られます:

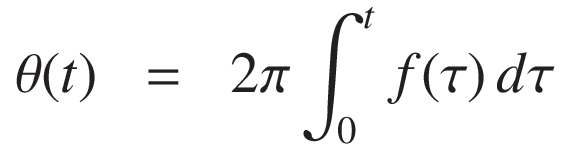
$\theta(t) &=& 2\pi \int_0^t f(\tau) \, d\tau$

リニアスイープ (Linear Frequency Sweep)

リニアスイープでは、周波数は f₀ から f₁ に時間 t_t とともに直線的に変化します。その瞬時周波数は次式で与えられます:

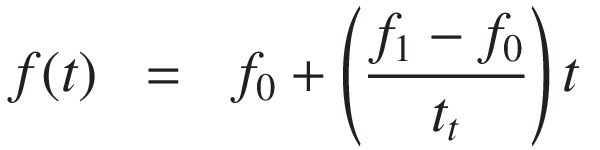
$f(t) &=& f_0 + \left( \frac{f_1 - f_0}{t_t} \right) t$

これを積分することで位相が得られます:

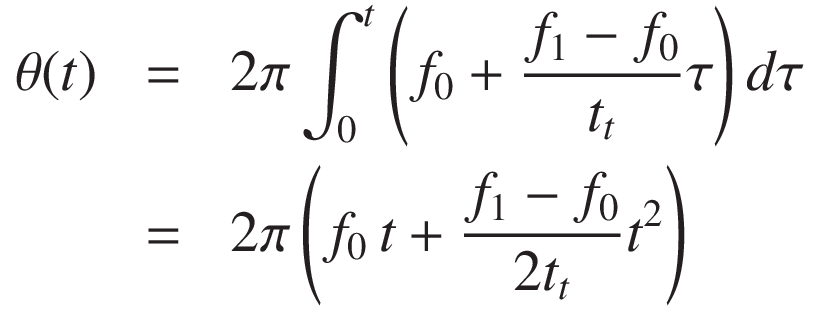
$\theta(t) &=& 2\pi \int_0^t \left( f_0 + \frac{f_1 - f_0}{t_t} \tau \right) d\tau\\ &=& 2\pi \left( f_0\, t + \frac{f_1 - f_0}{2t_t} t^2 \right)$

従って、リニアスイープの信号は次のように表されます:

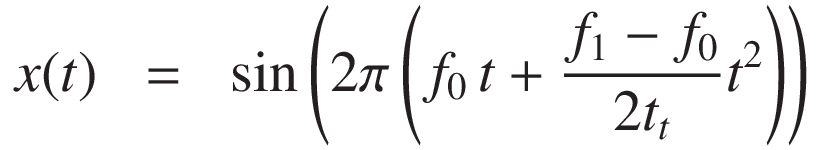
$x(t) &=& \sin\left( 2\pi \left( f_0\, t + \frac{f_1 - f_0}{2t_t} t^2 \right) \right)$

対数スイープ (Log Sweep)

対数（あるいは指数）スイープでは周波数が時間とともに指数的に変化します:

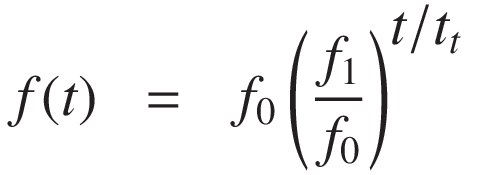
$f(t) &=& f_0 \left( \frac{f_1}{f_0} \right)^{\displaystyle{t / t_t}}$

r = f₁ / f₀ と置くと、積分により位相がえられます:

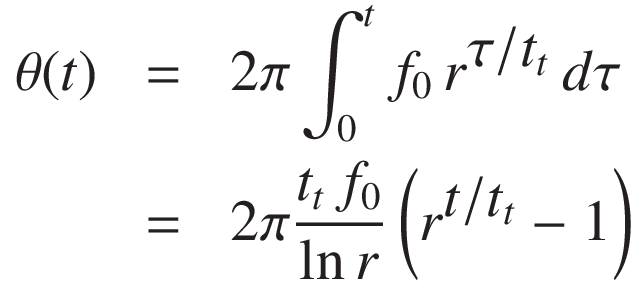
$\theta(t) &=& 2\pi \int_0^t f_0\, r^{\displaystyle{\tau / t_t}} \, d\tau\\ &=& 2\pi \frac{t_t\, f_0}{\ln r} \left( r^{\displaystyle{t / t_t}} - 1 \right)$

従って対数スイープの信号は次のように表されます:

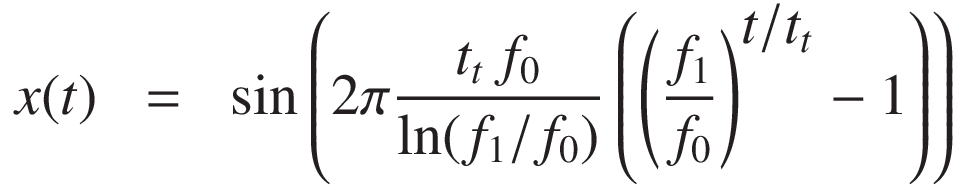
$x(t) &=& \sin\left( 2\pi \frac{t_t\, f_0}{\ln(f_1/f_0)} \left( \left(\frac{f_1}{f_0}\right)^{\displaystyle{t/t_t}} - 1 \right) \right)$

まとめ

重要な関係は次のものです:

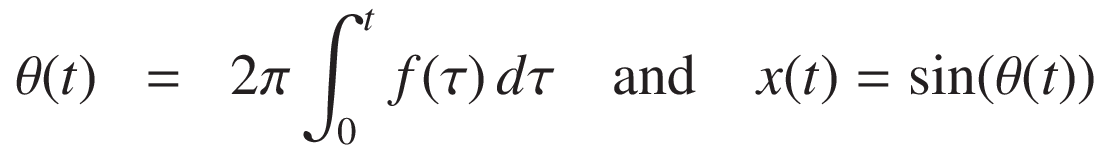
$\theta(t) &=& 2\pi \int_0^t f(\tau)\,d\tau \quad \text{and} \quad x(t) = \sin(\theta(t))$

この仕組みにより、信号解析やシステム同定や音響測定において不可欠な、時間とともに周波数が変化する正弦波信号を構築することができます。

周波数スイープの波形例

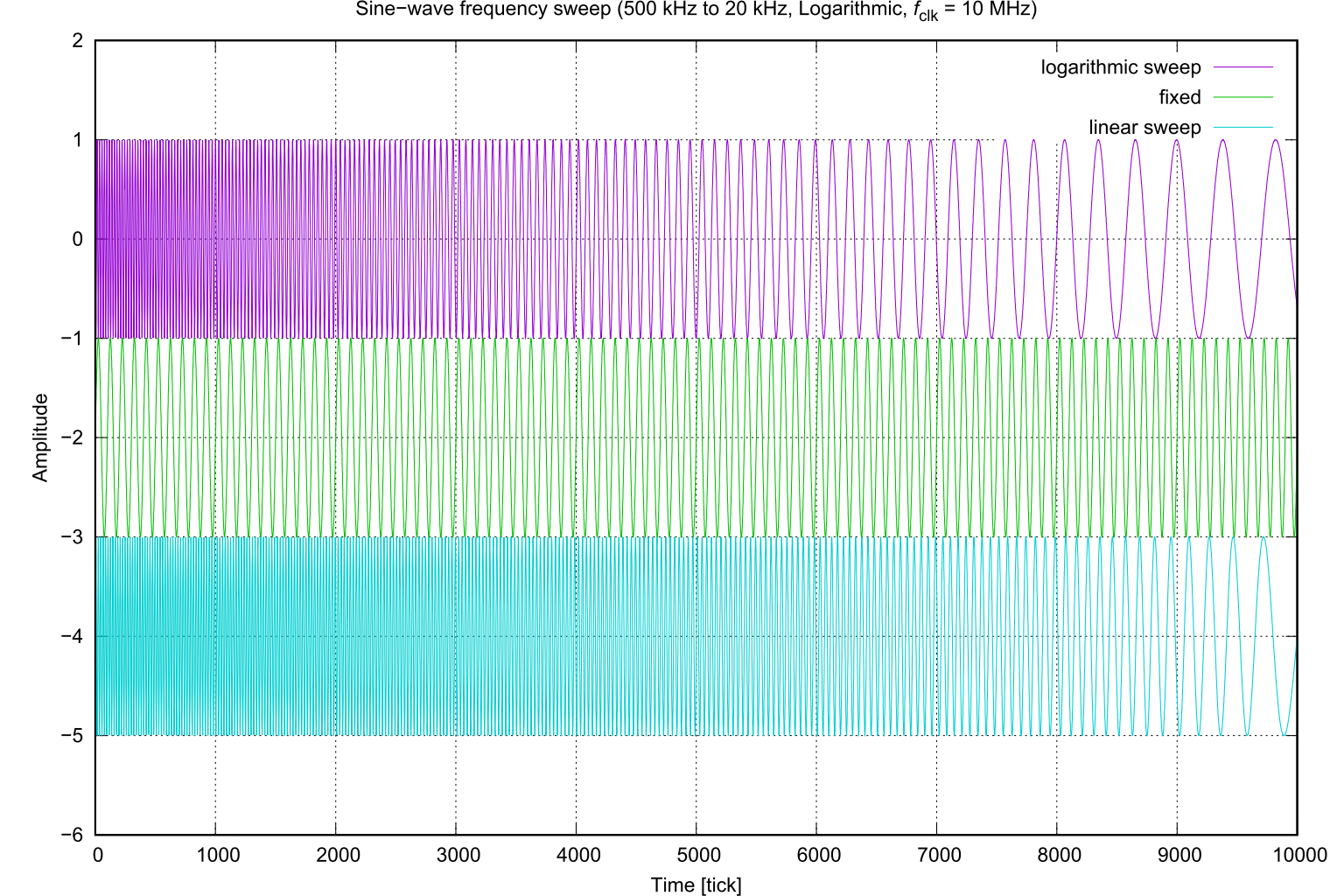
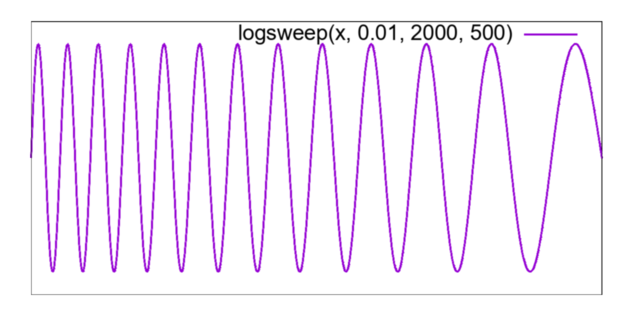
Fig. 1: 対数スイープ、固定、リニアスイープの波形

ソースコード例 C89 (ANSI-C)

Listing 1
sine_sweep - sine-wave frequency sweep. in C89 (ANSI-C)

/* sine_sweep : Sinusoidal wave frequency sweep 
 * Rev.1.0 (Oct. 18, 2012) (c) 2012 Takayuki Hosoda
 */
#include <math.h>

#define SWEEP_LIN    0
#define SWEEP_LOG    1

double sine_sweep(double t, double tt, double f0, double f1, int opt);

double
sine_sweep(t, tt, f0, f1, opt)
    double t;  /* time               */
    double tt; /* sweep time         */
    double f0; /* start frequency    */
    double f1; /* stop  frequency    */
    int opt;
{
    if (opt == SWEEP_LOG) {
        return sin(2 * M_PI * tt * f0 / log(f0 / f1) * (pow(f1 / f0, (t / tt)) - 1.0));
    } else {
        return sin(2 * M_PI * ((f1 - f0) * t * t / (2 * tt) + f0 * t));
    }
}

#ifdef DEBUG
#include <stdio.h>
int main() {
    int    t;
    double tt   = 10000;
    double fclk = 10e6;
    /* 0 - 10000 500kHz..20kHz log sweep */
    for (t = 0; t < 10000; t++) {
        printf("%d\t%.16g\t%.16g\t%.16g\n", t,
            sine_sweep((double)(t)/fclk, 10000/fclk, 500e3, 20e3, SWEEP_LOG),
            sine_sweep((double)(t)/fclk, 10000/fclk, 500e3, 20e3, SWEEP_LIN),
            sin(2*M_PI*t*100e3/fclk));
    }
    return 0;
}
#endif