Understanding Frequency Sweeps in sWaves

in C89
Understanding Frequency Sweeps in Sine Waves

#gnuplot 6.0
reset
unset xtics
unset ytics
set object 2 rect from graph 0, graph 0 to graph 1, graph 1 behind
set object 2 rect fc rgb

#gnuplot 6.0
reset
unset xtics
unset ytics
set object 2 rect from graph 0, graph 0 to graph 1, graph 1 behind
set object 2 rect fc rgb

October 10, 2012
Reviced : May 20, 2025
Takayuki HOSODA

Introduction

sine wave with a constant frequency is typically written as:

$x(t) &=& \sin(2\pi f t)$
Here: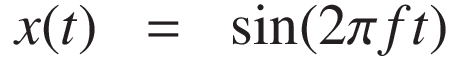

f is the frequency in Hz,
t is the time in seconds,
2πft is the angular phase in radians.

When the frequency varies with time—a process known as a frequency sweep—the general form of the signal becomes:

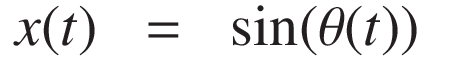
$x(t) &=& \sin(\theta(t))$

Where θ(t) is the time-dependent phase, which can be obtained by integrating the instantaneous frequency:

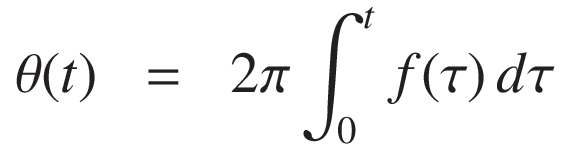
$\theta(t) &=& 2\pi \int_0^t f(\tau) \, d\tau$

Linear Frequency Sweep

In a linear sweep, the frequency increases linearly from f₀ to f₁ over a time interval t_t . The instantaneous frequency is given by:

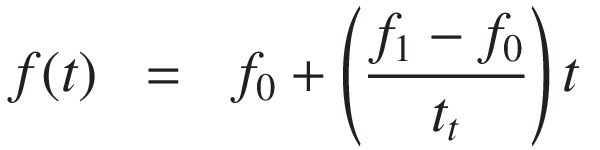
$f(t) &=& f_0 + \left( \frac{f_1 - f_0}{t_t} \right) t$

Integrating this, we obtain the phase:

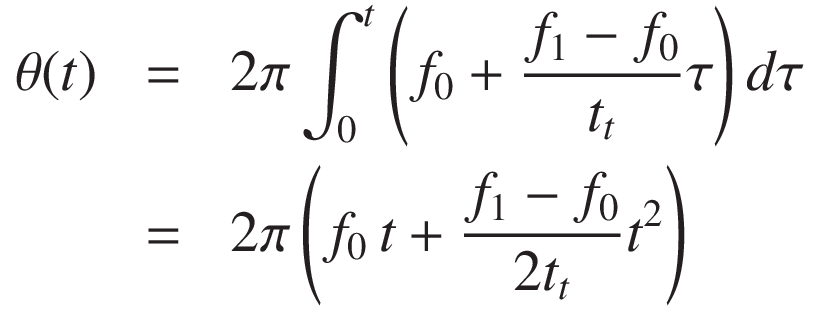
$\theta(t) &=& 2\pi \int_0^t \left( f_0 + \frac{f_1 - f_0}{t_t} \tau \right) d\tau\\ &=& 2\pi \left( f_0\, t + \frac{f_1 - f_0}{2t_t} t^2 \right)$

Therefore, the signal becomes:

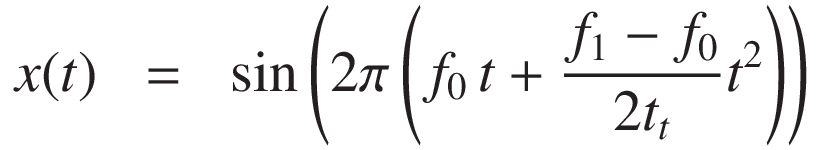
$x(t) &=& \sin\left( 2\pi \left( f_0\, t + \frac{f_1 - f_0}{2t_t} t^2 \right) \right)$

Logarithmic Frequency Sweep

In a logarithmic (or exponential) sweep, the frequency increases exponentially with time:

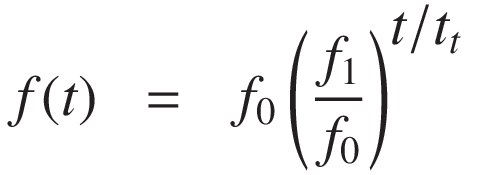
$f(t) &=& f_0 \left( \frac{f_1}{f_0} \right)^{\displaystyle{t / t_t}}$

Letting r = f₁ / f₀, we find the phase by integration:

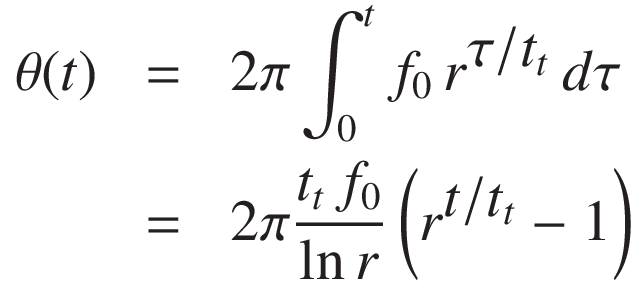
$\theta(t) &=& 2\pi \int_0^t f_0\, r^{\displaystyle{\tau / t_t}} \, d\tau\\ &=& 2\pi \frac{t_t\, f_0}{\ln r} \left( r^{\displaystyle{t / t_t}} - 1 \right)$

Hence, the logarithmic sweep signal is:

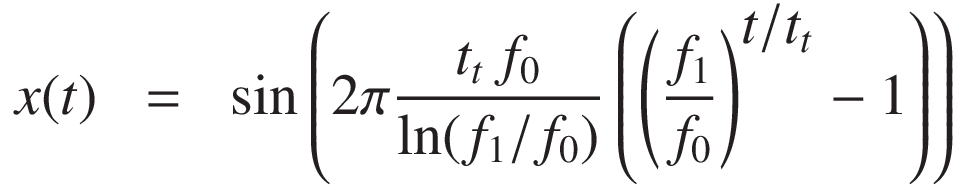
$x(t) &=& \sin\left( 2\pi \frac{t_t\, f_0}{\ln(f_1/f_0)} \left( \left(\frac{f_1}{f_0}\right)^{\displaystyle{t/t_t}} - 1 \right) \right)$

Summary

The key relationship is:

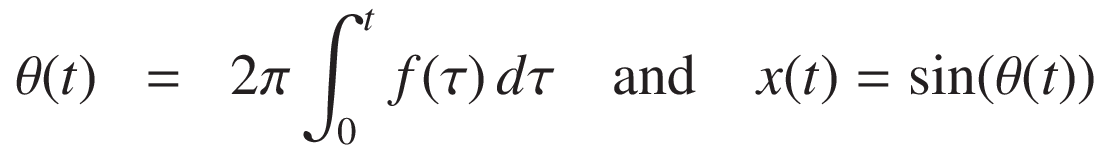
$\theta(t) &=& 2\pi \int_0^t f(\tau)\,d\tau \quad \text{and} \quad x(t) = \sin(\theta(t))$

This framework allows us to construct sine wave signals with time-varying frequencies, which are essential in signal analysis, system identification, and acoustic measurements.

Frequency sweep waveform

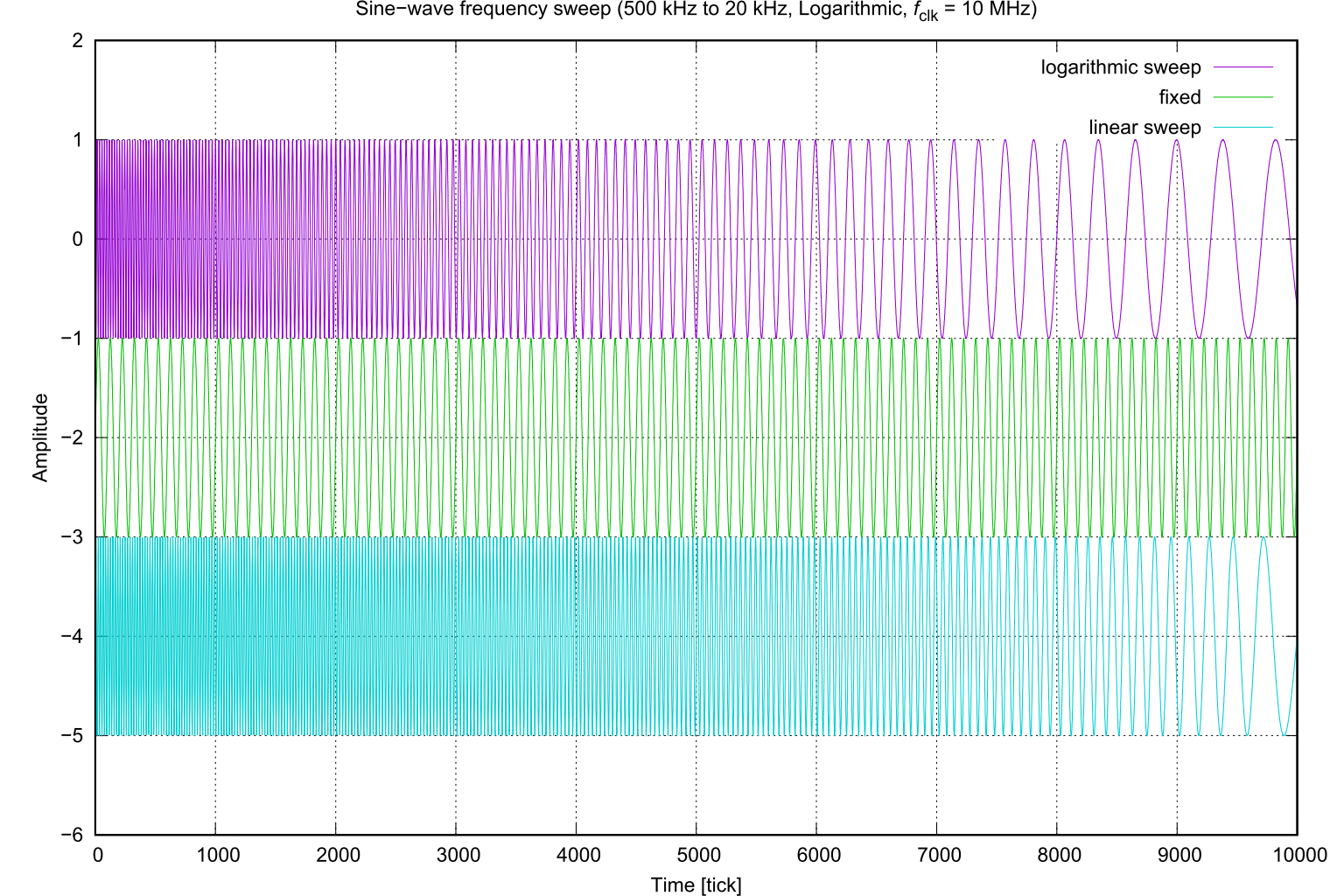
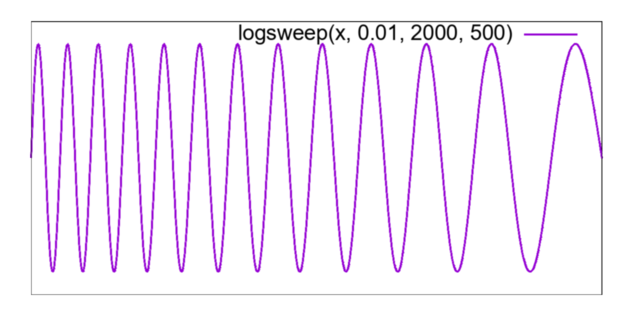
Fig. 1: Logarithmic, fixed and linear sweep waveforms

Source code in C89 (ANSI-C)

Listing 1
sine_sweep - sine-wave frequency sweep. in C89 (ANSI-C)

/* sine_sweep : Sinusoidal wave frequency sweep 
 * Rev.1.0 (Oct. 18, 2012) (c) 2012 Takayuki Hosoda
 */
#include <math.h>

#define SWEEP_LIN    0
#define SWEEP_LOG    1

double sine_sweep(double t, double tt, double f0, double f1, int opt);

double
sine_sweep(t, tt, f0, f1, opt)
    double t;  /* time               */
    double tt; /* sweep time         */
    double f0; /* start frequency    */
    double f1; /* stop  frequency    */
    int opt;
{
    if (opt == SWEEP_LOG) {
        return sin(2 * M_PI * tt * f0 / log(f0 / f1) * (pow(f1 / f0, (t / tt)) - 1.0));
    } else {
        return sin(2 * M_PI * ((f1 - f0) * t * t / (2 * tt) + f0 * t));
    }
}

#ifdef DEBUG
#include <stdio.h>
int main() {
    int    t;
    double tt   = 10000;
    double fclk = 10e6;
    /* 0 - 10000 500kHz..20kHz log sweep */
    for (t = 0; t < 10000; t++) {
        printf("%d\t%.16g\t%.16g\t%.16g\n", t,
            sine_sweep((double)(t)/fclk, 10000/fclk, 500e3, 20e3, SWEEP_LOG),
            sine_sweep((double)(t)/fclk, 10000/fclk, 500e3, 20e3, SWEEP_LIN),
            sin(2*M_PI*t*100e3/fclk));
    }
    return 0;
}
#endif