| Rational interpolation |
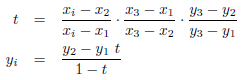
|
- REG X : x
- REG 01 : x1
- REG 02 : x2
- REG 03 : x3
- REG 04 : y1
- REG 05 : y2
- REG 06 : y3
- FLAG 01
- LBL "RI" : entry point
- REG 01~03: x values
- REG 04~06: y values
- REG Y : x
- REG X : y
RI - Rev.1.10 Sep. 30 2011 00 { 84-Byte Prgm } 01 LBL "RI" 02 ENTER 03 ENTER 04 ENTER 05 RCL 03 06 - 07 ABS 08 X<>Y 09 RCL- 01 10 ABS 11 - 12 CF 01 13 X>0? 14 SF 01 15 R↓ 16 RCL- 03 17 RCL 02 18 RCL- 01 19 × 20 RCL 05 21 RCL- 06 22 × 23 X<>Y 24 RCL- 01 25 RCL 02 26 RCL- 03 27 × 28 RCL 05 29 RCL- 04 30 × 31 FS? 01 32 X<>Y 33 X=0? 34 GTO E 35 ÷ 36 X<>Y 37 RCL 06 38 RCL 04 39 FS? 01 40 X<>Y 41 R↑ 42 × 43 LASTX 44 R↓ 45 - 46 1 47 R↑ 48 - 49 X=0? 50 GTO E 51 ÷ 52 RTN 53 LBL E 54 BEEP 55 RTN 56 .END.
'RI' (ri.raw, 87 byte, raw program file for the Free42)
Rational interpolation 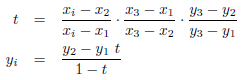
Note Interpolation
Common logarithmsReverse interpolation
Temperature V.S. Resistance characteristic of an NTC thermistorOperation Results
RI - Rational interpolation program for the HP 15C
Online calculator - Rational interpolation and Lagrange interpolation
Ostrowski's method - a root-finding method

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.