/* riali : An interpolation program. Rev.1.11 : Oct. 3, 2011
* Copyright (c) 2011, Takayuki HOSODA. All rights reserved.
*
* SYNOPSIS
* #include <math.h>
*
* double
* riali(double x[3], double y[3], double xi, int mode)
*
* RETURN VALUE
* The riali() function return NaN on errors.
*
* DESCRIPTION
* The riali() calculate univariate interpolation for xi from a set of three data points.
* The argument mode specifies interpolation method by one of the followings,
* AIP_RATIONAL : 1st/1st order rational interpolation
* AIP_LAGRANGE : 2nd order Lagrange interpolation
* AIP_AUTO : use rational interpolation when the set of data points is
* monotonic, otherwise use Lagrange interpolation instead.
* LINK
* http://www.finetune.jp/~lyuka/technote/riali/
*/
#include <math.h>
#define AIP_AUTO 0
#define AIP_RATIONAL 1
#define AIP_LAGRANGE 2
double
riali(x, y, xi, mode)
double x[3];
double y[3];
double xi;
int mode;
{
register double t, u;
if (y[0] == y[1] && y[1] == y[2]) return y[0];
if (mode == AIP_AUTO) {
if (x[0] > x[1]) {t = x[0]; x[0] = x[1]; x[1] = t; t = y[0]; y[0] = y[1]; y[1] = t;}
if (x[1] > x[2]) {t = x[1]; x[1] = x[2]; x[2] = t; t = y[1]; y[1] = y[2]; y[2] = t;}
if (x[0] > x[1]) {t = x[0]; x[0] = x[1]; x[1] = t; t = y[0]; y[0] = y[1]; y[1] = t;}
mode = ((y[0] < y[1] && y[1] < y[2]) || (y[0] > y[1] && y[1] > y[2])) ?
AIP_RATIONAL : AIP_LAGRANGE;
}
if (mode == AIP_RATIONAL) {
t = (xi - x[1]) * (x[2] - x[0]) * (y[2] - y[1]);
u = (xi - x[0]) * (x[2] - x[1]) * (y[2] - y[0]);
if ((t == 0.) && (u == 0)) return NAN;
if ( t == 0.) return y[1];
if ( u == 0.) return y[0];
if (fabs(x[1] - xi) < fabs(x[0] - xi)) {
t /= u; return (y[0] * t - y[1]) / (t - 1.0);
}
u /= t; return (y[1] * u - y[0]) / (u - 1.0);
} else {
if (x[0] == x[1] || x[1] == x[2] || x[2] == x[0]) return NAN;
t = y[0] * (xi - x[1]) * (xi - x[2]) / ((x[0] - x[1]) * (x[0] - x[2]));
t += y[1] * (xi - x[0]) * (xi - x[2]) / ((x[1] - x[0]) * (x[1] - x[2]));
t += y[2] * (xi - x[0]) * (xi - x[1]) / ((x[2] - x[0]) * (x[2] - x[1]));
return t;
}
}
#ifdef DEBUG
#include <stdio.h>
int
main()
{
int i;
double xi, yi;
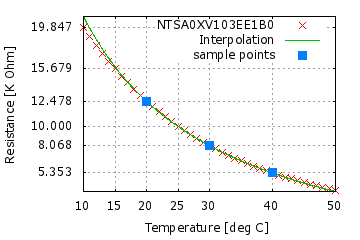
/* Resistance V.S. Temperature table of an NTC thermistor */
double x[6] = { 19.847, 12.478, 8.068, 5.353, 3.635 };
double y[6] = { 10.000, 20.000, 30.000, 40.00, 50.000 };
printf("Res.\tTemp.\tRelative error\n");
/*Extrapolation*/
yi = ri(&x[1], &y[1], xi = 15.679); printf("%g\t%g\t%g\n", xi, yi, yi/15. -1.);
/*Interpolation*/
yi = ri(&x[1], &y[1], xi = 12.478); printf("%g\t%g\t%g\n", xi, yi, yi/20. -1.);
yi = ri(&x[1], &y[1], xi = 10.000); printf("%g\t%g\t%g\n", xi, yi, yi/25. -1.);
yi = ri(&x[1], &y[1], xi = 8.068); printf("%g\t%g\t%g\n", xi, yi, yi/30. -1.);
yi = ri(&x[1], &y[1], xi = 6.552); printf("%g\t%g\t%g\n", xi, yi, yi/35. -1.);
yi = ri(&x[1], &y[1], xi = 5.353); printf("%g\t%g\t%g\n", xi, yi, yi/40. -1.);
/*Extrapolation*/
yi = ri(&x[1], &y[1], xi = 4.399); printf("%g\t%g\t%g\n", xi, yi, yi/45. -1.);
return 0;
}
#endif
|

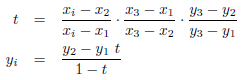

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.