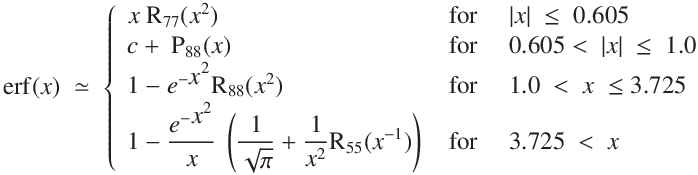80ビット拡張倍精度版 erfl()
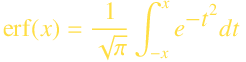
2023年3月12日
細田 隆之
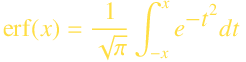
 English edition is here.
English edition is here.
list.1 [ erfl.c ]
Formulas used
但し
Rpq(z) と Ppq(z) は,分子の次数が p,分母の次数が q の有理多項式です.
c は展開点でのオフセット定数です.
/* erfl -- the error function * Rev.0.81 (Apr. 1, 2023) (c) 2023, Takayuki HOSODA * http://www.finetune.co.jp/~lyuka/technote/erf/erf.html */ #include <math.h> #include <float.h> #ifdef __FreeBSD__ #include <floatingpoint.h> #endif #ifdef HAVE_NO_FMAL #define fmal(x, y, z) ((long double)(x) * (long double)(y) + (long double)(z)) #endif long double expl(long double x); long double _erfl(long double x); /** _erfl() returns the error function of long double argument x. */ long double _erfl(long double x) { static const long double C_1_SQRTPI = 0.56418958354775628694807945156L; /* 1 / sqrt(pi) */ static const long double C_ERF4_5 = 0.74210096470766048616711058650L; /* erf(0.8) */ static const long double P16[8] = { -1.070994903454568471198625L, 6.699056619197806155096750e1L, 3.836872558121628370861145e2L, 2.330912586605424986344727e4L, 1.192715994130136754041117e5L, 1.364468800573643889138584e6L, 3.317475045249792251787123e6L, 1.786643811469380990926888e7L}; static const long double Q16[8] = { 2.941246331890315828828428e1L, 1.017359879433847453706309e3L, 1.668428796787451725830567e4L, 1.670786988026414025035867e5L, 1.096119220761948349285763e6L, 4.679646185985653079831373e6L, 1.196038392881251171811113e7L, 1.403226768173468723774884e7L}; static const long double P17[9] = { -1.319242994183035015890636L, 3.106509878983975077087577e1L, -1.745446871134725345560832e2L, 5.837496016170828196431911e2L, -1.048567241591721668860213e3L, 2.874128141559910487288155e3L, -7.604923107405640615105820e3L, 1.490084846047330072921859e4L, -8.247409164119979163956445e3L}; static const long double Q17[9] = { 3.950893779511369664081126L, -1.111857860661818708874906e1L, 1.044378982540079465540971e2L, -1.938357768620100743940678e2L, 1.082261956698468661417821e3L, -1.277774841563906386824489e3L, 5.411307109730631480478850e3L, -3.180834037722478451422939e3L, 1.111359445181890055153383e4L}; /* Coeficients below are from "Rational Chebyshev Approximations for the Error Fucntion", by W. J. Cody */ static const long double P2[9] = { 1.23033935479799725272e3L, 2.05107837782607146532e3L, 1.71204761263407058314e3L, 8.81952221241769090411e2L, 2.98635138197400131132e2L, 6.61191906371416294775e1L, 8.88314979438837594118e0L, 5.64188496988670089180e-1L, 2.15311535474403846343e-8L}; static const long double Q2[9] = { 1.23033935480374942043e3L, 3.43936767414372163696e3L, 4.36261909014324715820e3L, 3.29079923573345962678e3L, 1.62138957456669018874e3L, 5.37181101862009857509e2L, 1.17693950891312499305e2L, 1.57449261107098347253e1L, 1.0L}; static const long double P3[6] = { -6.58749161529837803157e-4L, -1.60837851487422766278e-2L, -1.25781726111229246204e-1L, -3.60344899949804439429e-1L, -3.05326634961232344035e-1L, -1.63153871373020978498e-2L}; static const long double Q3[6] = { 2.33520497626869185443e-3L, 6.05183413124413191178e-2L, 5.27905102951428412248e-1L, 1.87295284992346047209e0L, 2.56852019228982242072e0L, 1.0L}; long double a, s, sp, sq, y; int i; if (isnan(x)) return x; a = fabsl(x); switch (a <= 0.605L ? 16 : a <= 1.0L ? 17 : a <= 3.725L ? 2 : a <= 6.6L ? 3 : 4) { case 2: /* 1 - erfc(x), +4.15e-20 theoretical accuracy for 1.0 <= |x| */ sp = P2[8]; sq = Q2[8]; for (i = 7; i >= 0; i--) { sp = fmal(a, sp, P2[i]); /* sp = P2[i] + a * sp; */ sq = fmal(a, sq, Q2[i]); /* sq = Q2[i] + a * sq; */ } y = 1.0L - expl(-a * a) * sp / sq; /* erf(x) = 1 - erfc(x) */ break; case 3: /* 1 - erfc(x), +1.25e-22 theoretical accuracy for 3.725 <= |x| */ s = 1.0L / (a * a); sp = P3[5]; sq = Q3[5]; for (i = 4; i >= 0; i--) { sp = fmal(s, sp, P3[i]); /* sp = P3[i] + s * sp; */ sq = fmal(s, sq, Q3[i]); /* sq = Q3[i] + s * sq; */ } y = 1.0L - expl(-a * a) / a * (C_1_SQRTPI + s * sp / sq); /* erf(x) = 1 - erfc(x) */ break; case 16: /* -1.14e-21 theoretical accuracy for |x| <= 0.605 */ s = a * a; sp = P16[0]; sq = Q16[0]; for (i = 1; i < 8; i++) { sp = fmal(s, sp, P16[i]); /* sp = P16[i] + s * sp; */ sq = fmal(s, sq, Q16[i]); /* sq = Q16[i] + s * sq; */ } y = sqrtl(a * a * sp / sq); break; case 17: /* erf(x), +1.32e-21, -2.19e-21 theoretical accuracy for 0.605 <= |x| <= 1.0 */ sp = P17[0]; sq = Q17[0]; for (i = 1; i < 9; i++) { sp = fmal(a, sp, P17[i]); /* sp = P17[i] + a * sp; */ sq = fmal(a, sq, Q17[i]); /* sq = Q17[i] + a * sq; */ } y = C_ERF4_5 + sp / sq; /* erf(x) using pade approximation near x = 0.8 */ break; default: y = 1.0L; /* erfc(6.6) < 1.022e-20 < 0.1 * LDBL_EPSILON */ break; } if (x < 0) y = -y; return y; } #ifdef DEBUG_ERF #include <stdlib.h> #include <stdio.h> char *myname = "erfl"; char *revision = "Rev. 0.81 (Apr. 1, 2023)"; char *copyright = "(c) 2023, Takayuki HOSODA"; char *help = "Name\n\ erf -- returns the error function of real argument x.\n\ Usage\n\ erf x -- calculate erf(x) of real argument x."; long double cumu_dist(long double x) { static const long double C_SQRT1_2 = 0.707106781186547524400844362105L; /* 1 / sqrt(2) */ return 0.5L * (1.0L + _erfl(x * C_SQRT1_2)); } int main(int argc, char *argv[]) { long double x, y, e; char *dummy; int i, n, p; long double testvect[][2] = {\ {0.015625L, 0.017629489782642005545730159288245813L}, {0.03125L, 0.03525037386732282599861658807396349L}, {0.06250L, 0.07043197772238707805059005592329674L}, {0.12500L, 0.1403162048013338173930294465216234L}, {0.18750L, 0.2091176770593758483008706390019411L}, {0.25000L, 0.2763263901682369329850682677648157L}, {0.31250L, 0.3414686335015950062933371304950386L}, {0.37500L, 0.4041169094348222983238250859191218L}, {0.43750L, 0.4638981357499329730186612339181347L}, {0.46875L, 0.4926134732179379915881761019353467L}, {0.50000L, 0.5204998778130465376827466538919645L}, {0.56250L, 0.5736744566155919539905534671660978L}, {0.62500L, 0.6232408821884179724486405058767903L}, {0.68750L, 0.6690846628860812822284374988393579L}, {0.75000L, 0.7111556336535151315989378345914108L}, {0.81250L, 0.7494640255863620676101869621847319L}, {0.87500L, 0.7840750610598596583145357178988494L}, {0.93750L, 0.8151024010343998041769596488262749L}, {1.00000L, 0.8427007929497148693412206350826093L}, {1.25000L, 0.9229001282564582301365234811972811L}, {1.50000L, 0.9661051464753107270669762616459479L}, {2.00000L, 0.9953222650189527341620692563672529L}, {2.50000L, 0.9995930479825550410604357842600251L}, {3.00000L, 0.9999779095030014145586272238704177L}, {3.50000L, 0.9999992569016276585872544763162439L}, {4.00000L, 0.9999999845827420997199811478403265L}, {4.50000L, 0.9999999998033839558457112523720840L}, {5.00000L, 0.9999999999984625402055719651498117L}, {5.50000L, 0.9999999999999926421520820256019369L}, {6.00000L, 0.9999999999999999784802632875010869L}, {6.50000L, 0.9999999999999999999615785167287935L}, {7.00000L, 0.9999999999999999999999581617439222L}}; #ifdef __FreeBSD__ fpsetprec(FP_PE); fpsetround(FP_RN); #endif if (argc == 2) { x = strtold(argv[1], &dummy); y = _erfl(x); e = cumu_dist(x) - cumu_dist(-x); printf("erf(%.18Lg) ~= %18.18Lg, cdf(%.18Lg) ~= %18.18Lg\n", x, y, x, e); } else { printf("#%s %s %s\n", myname, revision, copyright); printf("#x \treferece value \terf(x) \treletive error\n"); n = sizeof(testvect) / (sizeof(testvect[0][0]) + sizeof(testvect[0][1])); for (i = p = 0; i < n; i++) { y = _erfl(testvect[i][0]); e = y / testvect[i][1] - 1.0L; printf("%.8Lf\t%.20Lf\t%.20Lf\t%+.9Lg", testvect[i][0], testvect[i][1], y, e); if (fabsl(e) <= (2 * LDBL_EPSILON)) { p++; printf("\n"); } else { printf("\tFAIL\n"); } } printf("# %d of %d test vectors passed.\n", p, n); } return(0); } #endif
Download erfl-0.81.tar.gz— source code archive
Cody の論文[1] に記載されている有理チェビシェフ近似の係数を用いて拡張倍精度で誤差関数の近似を計算すると, 0.5 ≤ |x| ≤ 0.66 の範囲で相対誤差がマシンイプシロンの4倍に達することがありました(下図参照). x = 0 付近で 7次:7次, |x| = 0.8 付近で 8次:8次のパデ近似を用いると, |x| ≤ 0.7 と 0.57 ≤ |x| ≤ 1.05 の範囲でそれぞれ機械イプシロン以内の相対誤差になりました.
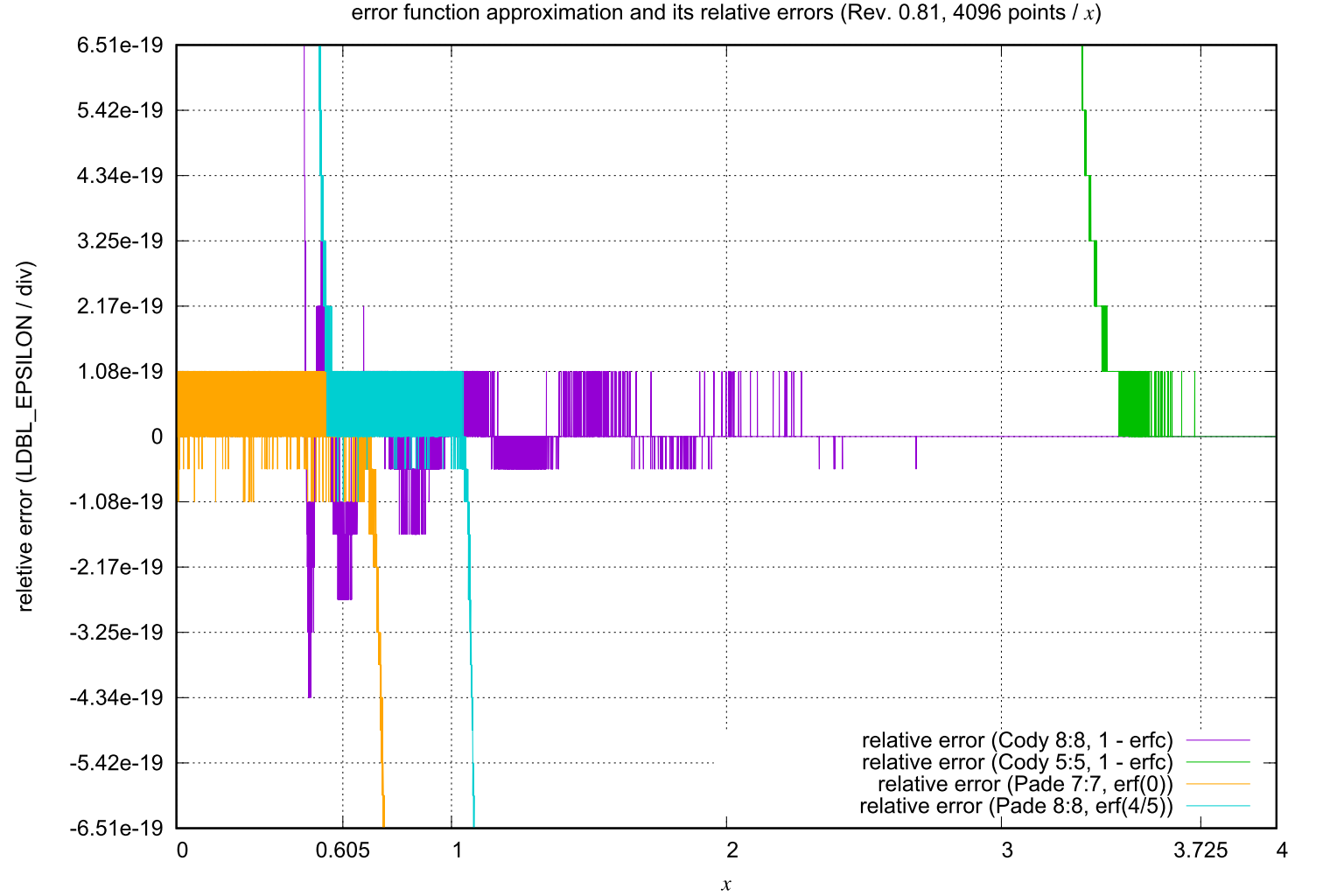
x の 4 つの範囲それぞれについて,適切な近似式を用いた拡張倍精度誤差関数の計算における相対誤差は,全範囲で機械イプシロン以内でした.
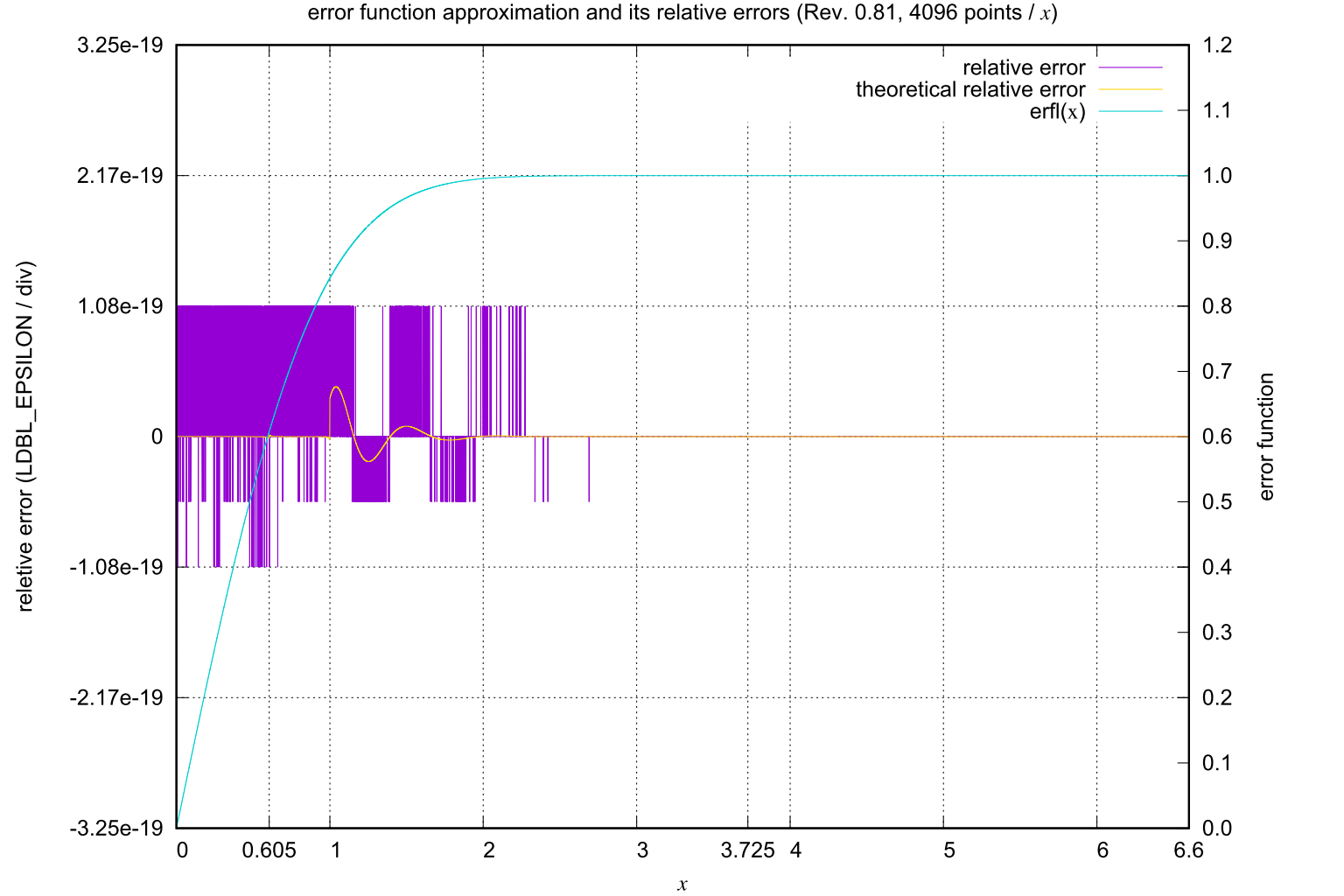
参考文献誤差関数は,標準分布の正規化積分を計算するために使用することができます.
標準正規分布の累積分布と誤差関数の計算

Download erf-0.35.js— source code

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.