/* erfl -- the error function
* Rev.0.81 (Apr. 1, 2023) (c) 2023, Takayuki HOSODA
* http://www.finetune.co.jp/~lyuka/technote/erf/erf.html
*/
#include <math.h>
#include <float.h>
#ifdef __FreeBSD__
#include <floatingpoint.h>
#endif
#ifdef HAVE_NO_FMAL
#define fmal(x, y, z) ((long double)(x) * (long double)(y) + (long double)(z))
#endif
long double expl(long double x);
long double _erfl(long double x);
/** _erfl() returns the error function of long double argument x. */
long double _erfl(long double x) {
static const long double C_1_SQRTPI = 0.56418958354775628694807945156L; /* 1 / sqrt(pi) */
static const long double C_ERF4_5 = 0.74210096470766048616711058650L; /* erf(0.8) */
static const long double P16[8] = {
-1.070994903454568471198625L,
6.699056619197806155096750e1L,
3.836872558121628370861145e2L,
2.330912586605424986344727e4L,
1.192715994130136754041117e5L,
1.364468800573643889138584e6L,
3.317475045249792251787123e6L,
1.786643811469380990926888e7L};
static const long double Q16[8] = {
2.941246331890315828828428e1L,
1.017359879433847453706309e3L,
1.668428796787451725830567e4L,
1.670786988026414025035867e5L,
1.096119220761948349285763e6L,
4.679646185985653079831373e6L,
1.196038392881251171811113e7L,
1.403226768173468723774884e7L};
static const long double P17[9] = {
-1.319242994183035015890636L,
3.106509878983975077087577e1L,
-1.745446871134725345560832e2L,
5.837496016170828196431911e2L,
-1.048567241591721668860213e3L,
2.874128141559910487288155e3L,
-7.604923107405640615105820e3L,
1.490084846047330072921859e4L,
-8.247409164119979163956445e3L};
static const long double Q17[9] = {
3.950893779511369664081126L,
-1.111857860661818708874906e1L,
1.044378982540079465540971e2L,
-1.938357768620100743940678e2L,
1.082261956698468661417821e3L,
-1.277774841563906386824489e3L,
5.411307109730631480478850e3L,
-3.180834037722478451422939e3L,
1.111359445181890055153383e4L};
/* Coeficients below are from "Rational Chebyshev Approximations for the Error Fucntion", by W. J. Cody */
static const long double P2[9] = {
1.23033935479799725272e3L,
2.05107837782607146532e3L,
1.71204761263407058314e3L,
8.81952221241769090411e2L,
2.98635138197400131132e2L,
6.61191906371416294775e1L,
8.88314979438837594118e0L,
5.64188496988670089180e-1L,
2.15311535474403846343e-8L};
static const long double Q2[9] = {
1.23033935480374942043e3L,
3.43936767414372163696e3L,
4.36261909014324715820e3L,
3.29079923573345962678e3L,
1.62138957456669018874e3L,
5.37181101862009857509e2L,
1.17693950891312499305e2L,
1.57449261107098347253e1L,
1.0L};
static const long double P3[6] = {
-6.58749161529837803157e-4L,
-1.60837851487422766278e-2L,
-1.25781726111229246204e-1L,
-3.60344899949804439429e-1L,
-3.05326634961232344035e-1L,
-1.63153871373020978498e-2L};
static const long double Q3[6] = {
2.33520497626869185443e-3L,
6.05183413124413191178e-2L,
5.27905102951428412248e-1L,
1.87295284992346047209e0L,
2.56852019228982242072e0L,
1.0L};
long double a, s, sp, sq, y;
int i;
if (isnan(x)) return x;
a = fabsl(x);
switch (a <= 0.605L ? 16 : a <= 1.0L ? 17 : a <= 3.725L ? 2 : a <= 6.6L ? 3 : 4) {
case 2: /* 1 - erfc(x), +4.15e-20 theoretical accuracy for 1.0 <= |x| */
sp = P2[8];
sq = Q2[8];
for (i = 7; i >= 0; i--) {
sp = fmal(a, sp, P2[i]); /* sp = P2[i] + a * sp; */
sq = fmal(a, sq, Q2[i]); /* sq = Q2[i] + a * sq; */
}
y = 1.0L - expl(-a * a) * sp / sq; /* erf(x) = 1 - erfc(x) */
break;
case 3: /* 1 - erfc(x), +1.25e-22 theoretical accuracy for 3.725 <= |x| */
s = 1.0L / (a * a);
sp = P3[5];
sq = Q3[5];
for (i = 4; i >= 0; i--) {
sp = fmal(s, sp, P3[i]); /* sp = P3[i] + s * sp; */
sq = fmal(s, sq, Q3[i]); /* sq = Q3[i] + s * sq; */
}
y = 1.0L - expl(-a * a) / a * (C_1_SQRTPI + s * sp / sq); /* erf(x) = 1 - erfc(x) */
break;
case 16: /* -1.14e-21 theoretical accuracy for |x| <= 0.605 */
s = a * a;
sp = P16[0];
sq = Q16[0];
for (i = 1; i < 8; i++) {
sp = fmal(s, sp, P16[i]); /* sp = P16[i] + s * sp; */
sq = fmal(s, sq, Q16[i]); /* sq = Q16[i] + s * sq; */
}
y = sqrtl(a * a * sp / sq);
break;
case 17: /* erf(x), +1.32e-21, -2.19e-21 theoretical accuracy for 0.605 <= |x| <= 1.0 */
sp = P17[0];
sq = Q17[0];
for (i = 1; i < 9; i++) {
sp = fmal(a, sp, P17[i]); /* sp = P17[i] + a * sp; */
sq = fmal(a, sq, Q17[i]); /* sq = Q17[i] + a * sq; */
}
y = C_ERF4_5 + sp / sq; /* erf(x) using pade approximation near x = 0.8 */
break;
default:
y = 1.0L; /* erfc(6.6) < 1.022e-20 < 0.1 * LDBL_EPSILON */
break;
}
if (x < 0)
y = -y;
return y;
}
#ifdef DEBUG_ERF
#include <stdlib.h>
#include <stdio.h>
char *myname = "erfl";
char *revision = "Rev. 0.81 (Apr. 1, 2023)";
char *copyright = "(c) 2023, Takayuki HOSODA";
char *help = "Name\n\
erf -- returns the error function of real argument x.\n\
Usage\n\
erf x -- calculate erf(x) of real argument x.";
long double cumu_dist(long double x) {
static const long double C_SQRT1_2 = 0.707106781186547524400844362105L; /* 1 / sqrt(2) */
return 0.5L * (1.0L + _erfl(x * C_SQRT1_2));
}
int
main(int argc, char *argv[]) {
long double x, y, e;
char *dummy;
int i, n, p;
long double testvect[][2] = {\
{0.015625L, 0.017629489782642005545730159288245813L},
{0.03125L, 0.03525037386732282599861658807396349L},
{0.06250L, 0.07043197772238707805059005592329674L},
{0.12500L, 0.1403162048013338173930294465216234L},
{0.18750L, 0.2091176770593758483008706390019411L},
{0.25000L, 0.2763263901682369329850682677648157L},
{0.31250L, 0.3414686335015950062933371304950386L},
{0.37500L, 0.4041169094348222983238250859191218L},
{0.43750L, 0.4638981357499329730186612339181347L},
{0.46875L, 0.4926134732179379915881761019353467L},
{0.50000L, 0.5204998778130465376827466538919645L},
{0.56250L, 0.5736744566155919539905534671660978L},
{0.62500L, 0.6232408821884179724486405058767903L},
{0.68750L, 0.6690846628860812822284374988393579L},
{0.75000L, 0.7111556336535151315989378345914108L},
{0.81250L, 0.7494640255863620676101869621847319L},
{0.87500L, 0.7840750610598596583145357178988494L},
{0.93750L, 0.8151024010343998041769596488262749L},
{1.00000L, 0.8427007929497148693412206350826093L},
{1.25000L, 0.9229001282564582301365234811972811L},
{1.50000L, 0.9661051464753107270669762616459479L},
{2.00000L, 0.9953222650189527341620692563672529L},
{2.50000L, 0.9995930479825550410604357842600251L},
{3.00000L, 0.9999779095030014145586272238704177L},
{3.50000L, 0.9999992569016276585872544763162439L},
{4.00000L, 0.9999999845827420997199811478403265L},
{4.50000L, 0.9999999998033839558457112523720840L},
{5.00000L, 0.9999999999984625402055719651498117L},
{5.50000L, 0.9999999999999926421520820256019369L},
{6.00000L, 0.9999999999999999784802632875010869L},
{6.50000L, 0.9999999999999999999615785167287935L},
{7.00000L, 0.9999999999999999999999581617439222L}};
#ifdef __FreeBSD__
fpsetprec(FP_PE);
fpsetround(FP_RN);
#endif
if (argc == 2) {
x = strtold(argv[1], &dummy);
y = _erfl(x);
e = cumu_dist(x) - cumu_dist(-x);
printf("erf(%.18Lg) ~= %18.18Lg, cdf(%.18Lg) ~= %18.18Lg\n", x, y, x, e);
} else {
printf("#%s %s %s\n", myname, revision, copyright);
printf("#x \treferece value \terf(x) \treletive error\n");
n = sizeof(testvect) / (sizeof(testvect[0][0]) + sizeof(testvect[0][1]));
for (i = p = 0; i < n; i++) {
y = _erfl(testvect[i][0]);
e = y / testvect[i][1] - 1.0L;
printf("%.8Lf\t%.20Lf\t%.20Lf\t%+.9Lg", testvect[i][0], testvect[i][1], y, e);
if (fabsl(e) <= (2 * LDBL_EPSILON)) {
p++;
printf("\n");
} else {
printf("\tFAIL\n");
}
}
printf("# %d of %d test vectors passed.\n", p, n);
}
return(0);
}
#endif
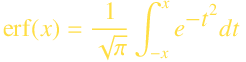
 Japanese edition is here.
Japanese edition is here.

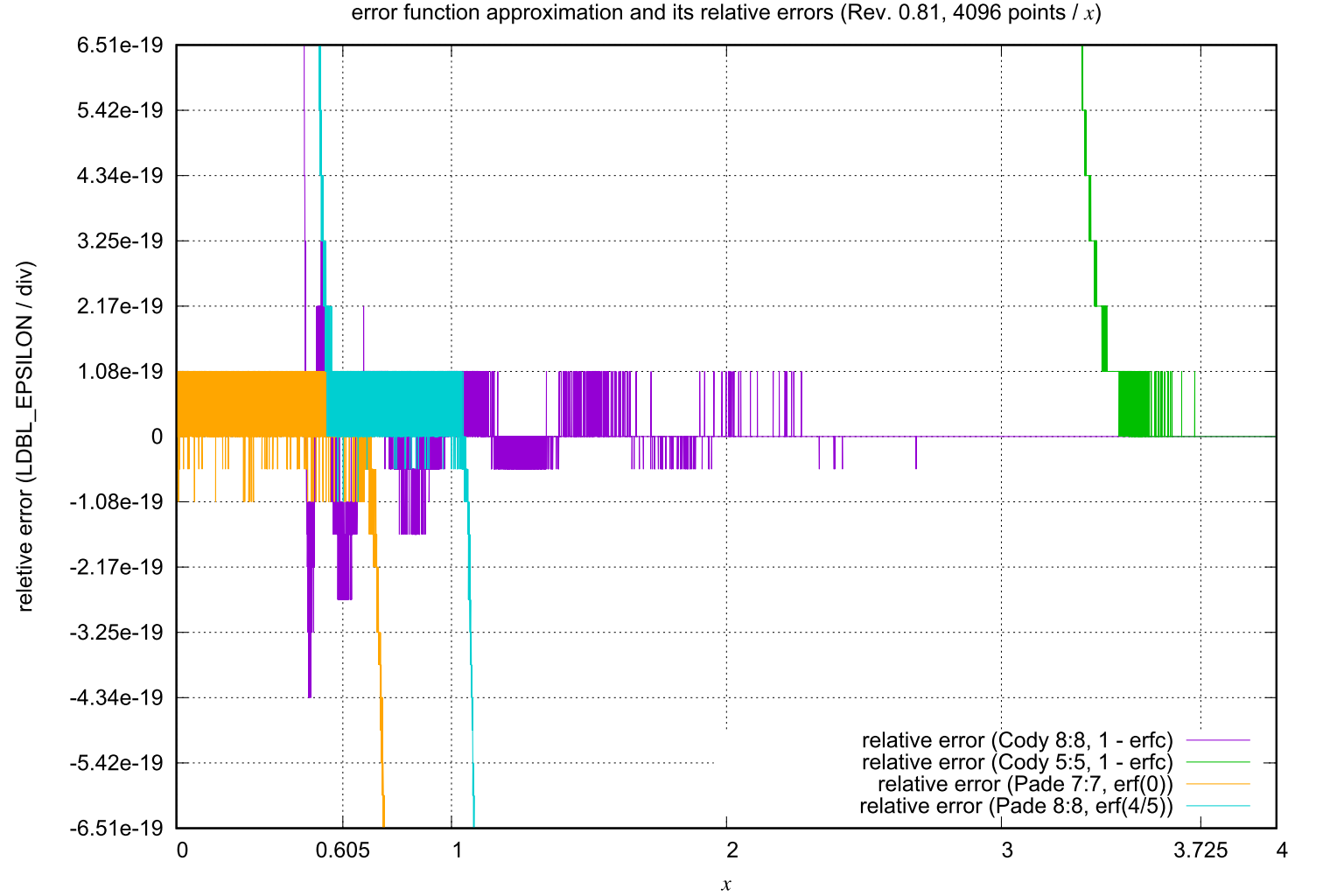
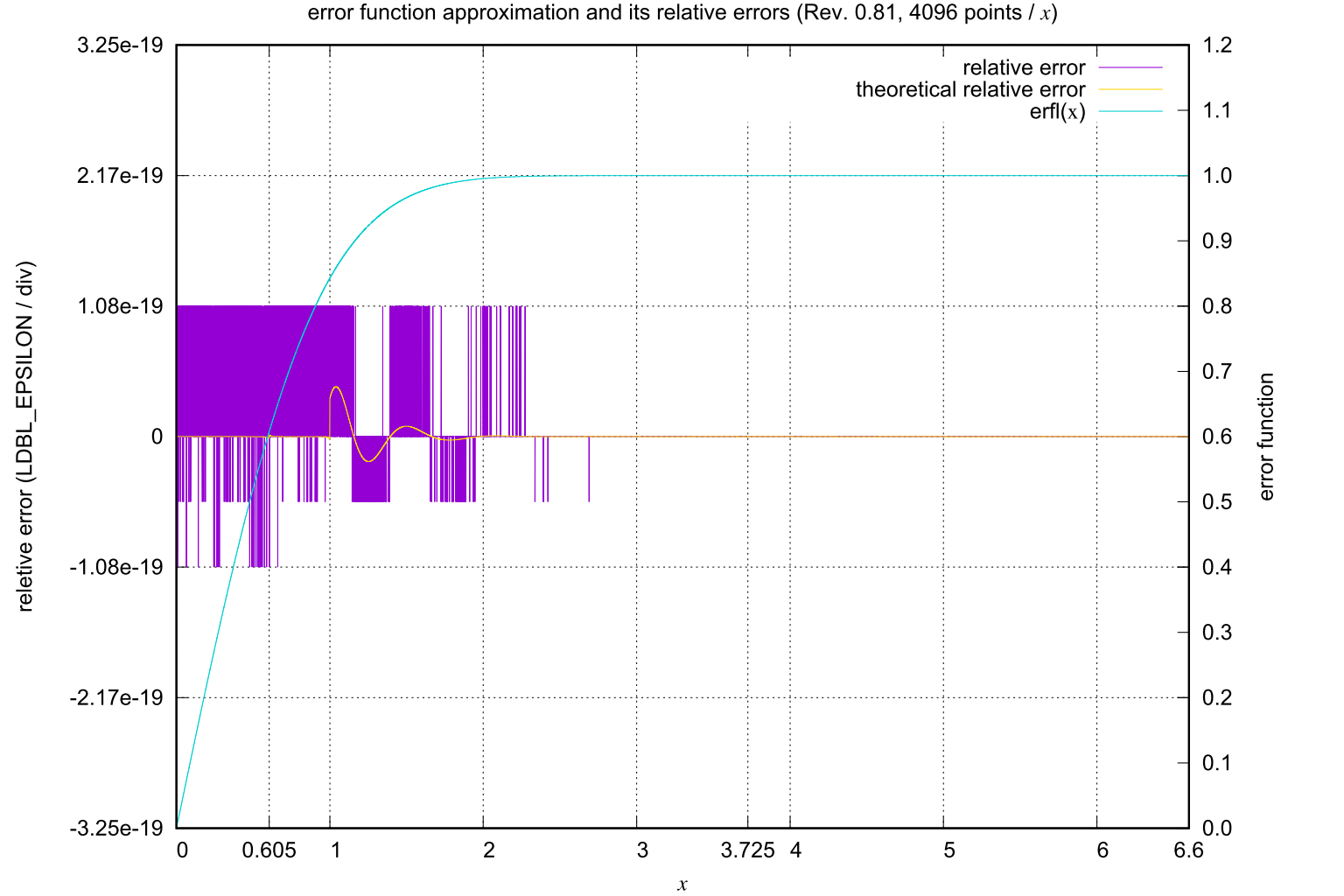


![[Mail]](/~lyuka/images/mail.gif)

 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.