in C99
80ビット拡張倍精度を使った０次第１種変形ベッセル関数 I0 の計算



2023年2月19日
細田 隆之
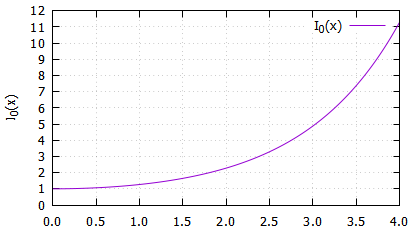
English English edition is here.

デジタル信号処理では、カイザー窓の計算などに０次の第１種修正ベッセル関数 I0 がよく使われますが、 制御変数 αが大きくなってくると I0 の値が指数関数的に大きくなって精度が低下し、 計算誤差がサイドローブ特性を悪化させることがあります。 そこで、I0 関数のいくつかの実装を比較し、80ビット拡張倍精度関数として実装した場合の誤差を調べました。

チェビシェフ (Chebyshev) 近似とパデ (Padé) 近似による I0 の計算

多くの I0 実装では、list.1の Formula Used にあるように、ある閾値で式を区切り、 多項式の係数をチェビシェフやパデ近似で最適化しています。 しかし、その倍精度計算への最適化が、拡張倍精度で I0 を計算したい場合には裏目に出てしまいます。

list.1 [ besi0q.c ]
Formulas used
I_0(x) \simeq \left\{ \begin{array}{ll} \displaystyle\frac{x^2}{4} \right \mathrm{P_{32}}\left(\displaystyle\frac{x^2}{4}\right) +1 \quad & \text{ for \quad$x \ < 15.5$}\\ \displaystyle\frac{e^x}{\sqrt{x}}\ \displaystyle{\frac{\mathrm{P_{45}}(x^{-1})}{\mathrm{P_{Q3}}(x^{-1})} }& \text{ for \quad $x \ge 15.5$}$} \end{array}
where

  P32(x), P45(x) and PQ3(x) are polynomials of corresponding degrees.
相対誤差の比較 


上記計算範囲での最大誤差 (0 ≤ x ≤ 40.0)
    gsl_sf_bessel_I0 : 8.182e-16 (x = 19.0859375)
    nr3_i0           : 5.534e-16 (x = 15.0009765625)
    _besi0p          : 6.353e-17 (x = 33.8134765625)
    _besi0q          : 2.494e-18 (x = 38.1123046875)

Note. gsl_sf_bessel_I0(x) overflows when x > 708.78271289338391628L.

無限級数と多項式近似による I0 の計算

I0(x) は x = 0 付近と x = ∞ 付近で無限級数として表現できるので、 2つの無限級数計算を切り替えるポイントを適切に選択すれば、 計算時間の多少の増加で直接計算で拡張倍精度の値を得ることができます。

list.2 [ besi0l.h, besi0l.c ]
NAME
    besi0l(x) the 0th-order modified Bessel function of the first kind I0
SYNOPSIS
    #include <math.h>
    #include <float.h>
    long double
    besi0l(long double x);
RETURN VALUE
    besi0l(x) returns the 0th-order modified Bessel function of the first kind of real argument x.
Formulas used
Definition :
  I_0(x) & = & \sum_{k = 0}^\infty \displaystyle\frac{1}{(k!)^2} \left(\frac{x}{2}\right) ^{2k}

Approximation :
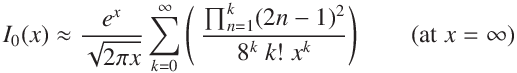
  I_0(x) \approx \frac{e^x}{ \sqrt{2 \pi x} }\sum_{k = 0}^ \infty \left(\displaystyle\ \frac{\prod_{n=1}^{k} (2n - 1)^2} {8^k \ k! \ x^k}\right) \qquad (\mathrm{at}\ x = \infty )
 Download besi0l-1.4.3.tar.gz — source code archive
相対誤差の比較（besi0l の無限級数部） 


上記計算範囲での最大誤差 (0 ≤ x ≤ 128.0)
    _besi0q         : 7.373e-18 (x = 125.7890625)
    _besi0l         : 4.879e-19 (x = 68.6015625)

計算速度の比較
    _besi0l : 1283 [ms] (0 ≤ x ≤  15.0, ittr = 10000000)
    _besi0q :  704 [ms] (0 ≤ x ≤  15.0, ittr = 10000000)
    _besi0l : 1246 [ms] (0 ≤ x ≤ 128.0, ittr = 10000000)
    _besi0q : 1227 [ms] (0 ≤ x ≤ 128.0, ittr = 10000000)

x がそれほど大きくない場合、I0(x) は無限級数を使って計算することができます。 無限級数加算におけるアンダーフローの影響を軽減するため、list.2 の _besi0l() の実装では、加算を主要部とマイナー部に分けています。 x が 64以下であれば I0(x) は 81回以下の繰り返しで計算できるので、 list.3 のように 81 * (3mul + 1div) の計算が浮動小数点ユニットで行われて、 コードがレベル１キャッシュの小さな部分に収まるのであれば、それは最新のプロセッサではそれほど悪いことではありません。 カイザー窓への応用という点では、 0 ≤ x ≤ 20π < 64 が α < 20 に相当し、ほとんどの実用的な目的には十分です。

list.3 [ 内側ループのアセンブリコード例 ] 
L25:
        fxch    %st(2)
.L9:
        movl    %eax, -128(%rsp)
        addl    $1, %eax
        fildl   -128(%rsp)
        fdivr   %st(4), %st
        fmul    %st(0), %st
        fmulp   %st, %st(2)
        fxch    %st(2)
        fadd    %st(1), %st
        fld     %st(0)
        fmul    %st(3), %st
        fcomip  %st(2), %st
        jb      .L25
Relative error comparison (besi0l polynomial approximation part)


Maximum errors in the calculations shown above. (0 ≤ x ≤ 768.0)
    _besi0q         : 5.312e-17 (x = 759.74609375)
    _besi0l         : 4.337e-19 (x = 68.6015625)

list.1 の besi0q() で x > 15.5 での誤差が大きくなっているのは、主に最後の expl() 計算に起因するものです。 list.2 の_besi0l() では、x > 24.0 に対する最後の expl() のレンジ・リダクションにより、誤差が大きく減少しています。

相対誤差の比較 (expl() のレンジ・リダクションの効果)

besi0q() も同様に、上記のように最後の expl() のレンジ・リダクションにより、x ≥ 15.5 での誤差を大幅に縮小することができました。

結論

I0 の応用の話として、カイザーウィンドウでよく使われる α が 3〜12 の範囲 — I0(x) の引数が π倍されて 9.42〜37.7 になる — でも、 テストした 64ビット倍精度版の I0(x) 関数すべての相対誤差は DBL_EPSILON（≒ 2.22 × 10-16 ）の 16倍以上でした。

80ビット拡張倍精度の実装では、計算誤差が大きく改善されないものもありました。 しかし、4倍精度の有理数近似の係数を使用するものは、 倍精度の表現範囲を超える 0 ≤ x ≤ 768 の範囲において、LDBL_EPSILON の 6倍（≒1.084 × 10-19）以内の誤差であることが示されました。

一方、_besi0l() では、LDBL_EPSILON の約 4.5倍の最大誤差で、拡張倍精度には実はオーソドックスな実装が適していることがわかりました。

おまけ

I0 calculator
x    I0 (x) ≈ 
 Download besi0l-1.4.3.js — source code 
I0 の参照値
I0(1)   ≃ 1.266065877752008335598244625214718
I0(2)   ≃ 2.279585302336067267437204440811533
I0(4)   ≃ 11.30192195213633049635627018321710
I0(8)   ≃ 427.5641157218047851773967913180829
I0(16)  ≃ 893446.2279201050170708640309761884
I0(32)  ≃ 5590908381350.873086500103776088605
I0(64)  ≃ 3.115457918187897557650694682306942 ×1026
I0(128) ≃ 1.372222546128743649356014388474097 ×1054
参考文献
  1. Pavel Holoborodko, "Rational Approximations for the Modified Bessel Function of the First Kind — I0(x) for Computations with Double Precision", November 11, 2015, Advanpix
  2. Modified Bessel Function of the First Kind — Wolfram MathWorld
  3. Bessel function / Modified_Bessel_functions: Iα,Kα — Wikipedia
  4. GSL Special Functions — GNU Scientific Library
  5. Numerical Recipes Webnote No.7, Rev.1, "Coefficients Used in the Bessjy and Bessik Objects" — Numerical Recipes
  6. I0(x) — WolframAlpha
www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.