in C99
I0 the 0th-order modified Bessel function of the First kind
besi0l() for extended double precision



Feb. 19, 2023
Takayuki HOSODA
Japanese Japanese edition is here.

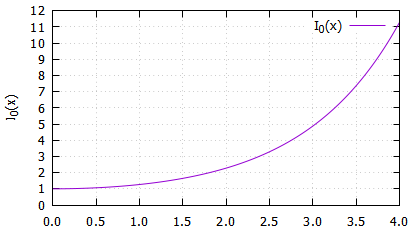
I0 the zeroth-order modified Bessel functions of the first kind are often used in digital signal processing to calculate, for example, the Kaiser window, but when the control variable α is getting large, the value of I0 becomes exponentially large, degrading accuracy, and the calculation error may worsen sidelobe characteristics. Therefore, we compared several implementations of the I0 function and investigated the error when they were implemented as 80-bit extended-double functions.

I0 calculation by Chebyshev and Padé approximations

In many I0 implementations, the formulas are separated at a certain threshold and the coefficients of the polynomial are optimized by Chebyshev or Padé approximation, as shown in Formulas Used in list.1. However, that double-precision optimized computation backfires when you want to calculate I0 in extended double precision.

list.1 [ besi0q.c ]
Formulas used
I_0(x) \simeq \left\{ \begin{array}{ll} \displaystyle\frac{x^2}{4} \right \mathrm{P_{32}}\left(\displaystyle\frac{x^2}{4}\right) +1 \quad & \text{ for \quad$x \ < 15.5$}\\ \displaystyle\frac{e^x}{\sqrt{x}}\ \displaystyle{\frac{\mathrm{P_{45}}(x^{-1})}{\mathrm{P_{Q3}}(x^{-1})} }& \text{ for \quad $x \ge 15.5$}$} \end{array}
where

  P32(x), P45(x) and PQ3(x) are polynomials of corresponding degrees.
Relative error comparison 


Maximum errors in the calculations shown above. (0 ≤ x ≤ 40.0)
    gsl_sf_bessel_I0 : 8.182e-16 (x = 19.0859375)
    nr3_i0           : 5.534e-16 (x = 15.0009765625)
    _besi0p          : 6.353e-17 (x = 33.8134765625)
    _besi0q          : 2.494e-18 (x = 38.1123046875)

Note. gsl_sf_bessel_I0(x) overflows when x > 708.78271289338391628L.

I0 calculation by infinite series and polynomial approximation

Since I0(x) can be expressed as an infinite series near x = 0 and near x = ∞, by appropriately choosing the point at which to switch between the two infinite series calculations, a direct calculation could yield values with extended double precision if a modest increase in computation time is allowed.

list.2 [ besi0l.h, besi0l.c ]
NAME
    besi0l(x) the 0th-order modified Bessel function of the first kind I0
SYNOPSIS
    #include <math.h>
    #include <float.h>
    long double
    besi0l(long double x);
RETURN VALUE
    besi0l(x) returns the 0th-order modified Bessel function of the first kind of real argument x.
Formulas used
Definition :
  I_0(x) & = & \sum_{k = 0}^\infty \displaystyle\frac{1}{(k!)^2} \left(\frac{x}{2}\right) ^{2k}

Approximation :
  I_0(x) \approx \frac{e^x}{ \sqrt{2 \pi x} }\sum_{k = 0}^ \infty \left(\displaystyle\ \frac{\prod_{n=1}^{k} (2n - 1)^2} {8^k \ k! \ x^k}\right) \qquad (\mathrm{at}\ x = \infty )
 Download besi0l-1.4.3.tar.gz — source code archive
Relative error comparison (besi0l infinite series part) 


Maximum errors in the calculations shown above. (0 ≤ x ≤ 128.0)
    _besi0q         : 7.373e-18 (x = 125.7890625)
    _besi0l         : 4.879e-19 (x = 68.6015625)

Calculation speed comparison
    _besi0l : 1283 [ms] (0 ≤ x ≤  15.0, ittr = 10000000)
    _besi0q :  704 [ms] (0 ≤ x ≤  15.0, ittr = 10000000)
    _besi0l : 1246 [ms] (0 ≤ x ≤ 128.0, ittr = 10000000)
    _besi0q : 1227 [ms] (0 ≤ x ≤ 128.0, ittr = 10000000)

If x is not so large, I0(x) can be calculated using an infinite series. In order to reduce the effect of underflow in infinite series addition, we divide the addition into two parts, the major part and the minor part, in our implimentation _besi0l() in list.2. If x is 64 or less, I0(x) can be computed in less than 81 iterations, so if 81 * (3mul + 1div) calculations are done in the floating-point unit as shown in list.3 and the code fits in a small portion of the Level-1 cache, it is not so bad for a modern processor. In terms of application to Kaiser windows, 0 ≤ x ≤ 20π < 64 corresponds to α < 20 and is sufficient for most practical purposes.

list.3 [ Assembly code example of the inner loop ] 
L25:
        fxch    %st(2)
.L9:
        movl    %eax, -128(%rsp)
        addl    $1, %eax
        fildl   -128(%rsp)
        fdivr   %st(4), %st
        fmul    %st(0), %st
        fmulp   %st, %st(2)
        fxch    %st(2)
        fadd    %st(1), %st
        fld     %st(0)
        fmul    %st(3), %st
        fcomip  %st(2), %st
        jb      .L25
Relative error comparison (besi0l polynomial approximation part)


Maximum errors in the calculations shown above. (0 ≤ x ≤ 768.0)
    _besi0q         : 5.312e-17 (x = 759.74609375)
    _besi0l         : 4.337e-19 (x = 68.6015625)

The increase of error in besi0q() in list.1 for x > 15.5 is mainly due to the calculation of the last expl() calculation.
In our implimentation _besi0l() in list.2, the range reduction at the last expl() calculation for x > 24.0 greatly reduces the error.

Relative error comparison (Effect of range reduction when using expl())

besi0q() was similarly able to greatly reduce the error for x ≥ 15.5 by range reduction in the last expl() as shown above.

Conclusion

As for the I0 application story, for α of 3 ~ 12, which is often used in the Kaiser window, the argument of I0(x) is multiplied by π to 9.42~ 37.7… Even in this range, the relative error of all 64-bit double versions of the I0(x) function tested was more than 16 times larger than DBL_EPSILON (≈ 2.22×10-16).

In the implementation of the 80-bit extended double precision, some of them did not show significant improvement in computational errors. However, one of them that uses coefficients of quadruple-precision rational approximation has been shown to have errors within 6 times LDBL_EPSILON (≈ 1.084×10-19) for the range of 0 ≤ x ≤ 768, which exceeds the range represented by double precision.

On the other hand, _besi0l() showed a maximum error of about 4.5 times that of LDBL_EPSILON, indicating that the orthodox implementation is actually suitable for extended double precision.

APPENDIX

I0 calculator
x    I0 (x) ≈ 
 Download besi0l-1.4.3.js — source code 
Reference values of I0
I0(1)   ≃ 1.266065877752008335598244625214718
I0(2)   ≃ 2.279585302336067267437204440811533
I0(4)   ≃ 11.30192195213633049635627018321710
I0(8)   ≃ 427.5641157218047851773967913180829
I0(16)  ≃ 893446.2279201050170708640309761884
I0(32)  ≃ 5590908381350.873086500103776088605
I0(64)  ≃ 3.115457918187897557650694682306942 ×1026
I0(128) ≃ 1.372222546128743649356014388474097 ×1054
REFERENCE
  1. Pavel Holoborodko, "Rational Approximations for the Modified Bessel Function of the First Kind — I0(x) for Computations with Double Precision", November 11, 2015, Advanpix
  2. Modified Bessel Function of the First Kind — Wolfram MathWorld
  3. Bessel function / Modified_Bessel_functions: Iα,Kα — Wikipedia
  4. GSL Special Functions — GNU Scientific Library
  5. Numerical Recipes Webnote No.7, Rev.1, "Coefficients Used in the Bessjy and Bessik Objects" — Numerical Recipes
  6. I0(x) — WolframAlpha
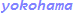
www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.