🌐English

パデ近似に基づく高精度・拡張倍精度 逆正接関数の実装

有理近似による数値精度と命令レベル並列性のバランス

2026-01-23
細田　隆之

概要

このページでは、X86 拡張倍精度（Extended-precision / 80ビット）演算をターゲットとした ANSI C（C89）によるアークタンジェント（arc tangent ; 逆正接）関数の実装を紹介します。 初等関数では多項式近似が一般的に用いられますが、 この実装ではパデ近似（Padé approximation ; 有理近似）を採用することで、 数値精度と最新のスーパースケーラ（superscalar）プロセッサの効率的な利用を両立させています。 分子と分母を独立に評価することで、中核となる近似は命令レベル並列処理（ILP, Instruction-Level Parallelism）や、 現代の CPU で利用可能な積和演算（FMA, fused multiply–add）パイプラインに適しています。 主要区間における理論誤差（絶対値）は 6.5×10-23 未満に抑えられていて、 アークタンジェントの恒等式に基づく引数削減と組み合わせることで、 この実装は値域全体にわたって高い精度を実現しています。 この設計は、移植性、予測可能性、アーキテクチャへの対応を重視していて、 高品質な libm 実装やパフォーマンス重視の数値ソフトウェアに適しています。

X86 Extended-Precision implementation (80-bit)

Listing 2: _atanl — arc tangent function in C89 (ANSI C) 
/* _atanl -- arc tangent function in C89 (ANSI-C), X86 Extended-precision (80-bit)
 * _atanl Rev.1.21 (Jan. 22, 2026) (c) 2007-2026 Takayuki HOSODA
 * SPDX-License-Identifier: BSD-3-Clause
 */
#include <math.h>
#include <float.h>

#define Q_SQRT2  1.41421356237309504880168872421L
#define Q_PI_2   1.57079632679489661923132169164L
#define Q_PI_4   0.78539816339744830961566084582L
#ifndef LDBL_EPSILON
#define LDBL_EPSILON   1.0842021724855044340E-19L
#endif

long double _atanl(long double x);
/* _atanl(x) computes the principal value of the arc tangent of x. */
long double _atanl(long double x) {
    long double q, s, v, w;
    long double offset = 0;
    if (x == 0) return x;
    if (x >  (2 / LDBL_EPSILON)) return  Q_PI_2;
    if (x < -(2 / LDBL_EPSILON)) return -Q_PI_2;
    if ((v = fabs(x)) >= 1) {
        if (v > Q_SQRT2 + 1.0L) {
            offset = -Q_PI_2; v = 1 / v;
        } else {
            offset =  Q_PI_4; v = (v - 1) / (1 + v);
        }
    } else if (v > Q_SQRT2 - 1.0L) {
            offset = -Q_PI_4; v = (1 - v) / (1 + v);
    }  /* Argument reduction into four regions using atan identities */
    s = v * v;
    w =               29360128.L; q =            27923620725.L;
    w = w * s +    23930643317.L; q = q * s +   742768311285.L;
    w = w * s +   501165956970.L; q = q * s +  6684914801565.L;
    w = w * s +  3525222266475.L; q = q * s + 28472785265925.L;
    w = w * s + 11362119869100.L; q = q * s + 64710875604375.L;
    w = w * s + 18420316154955.L; q = q * s + 80639706522375.L;
    w = w * s + 14615037006570.L; q = q * s + 51967810869975.L;
    w = w * s +  4512611027925.L; q = q * s + 13537833083775.L;
    w = w * s;  /* (14,14) Pade approximation for atan(x) / x - 1 */
    v -= w / q * v;  /* atan(x) = x - (atan(x) / x - 1) * x */
    s = v + offset;  /* |err| < 1.43e-21, x in [0, sqrt(2) - 1] */
    return (offset * x >= 0) ? (offset != 0 || x >= 0) ? s : -v: -s;
}

Empirical Error Analysis (80-bit)

In an empirical evaluation conducted using GCC 7.5, the custom _atanl function was tested on 65536 (= 216) uniformly spaced points per unit interval for x ∈ [0, 8] in long double-precision values. The relative error, computed as _atanl(x) / atanref(x) - 1 was found to be within ± 1.0842021724855044340E-19L, approximately the machine epsilon for IEEE 754 long double precision. Where atanref(x) denotes a rounded high-precision reference (≈ 40 digits), not a libm result.

For |x| > 8, argument reduction ensures that approximation errors rapidly diminish.

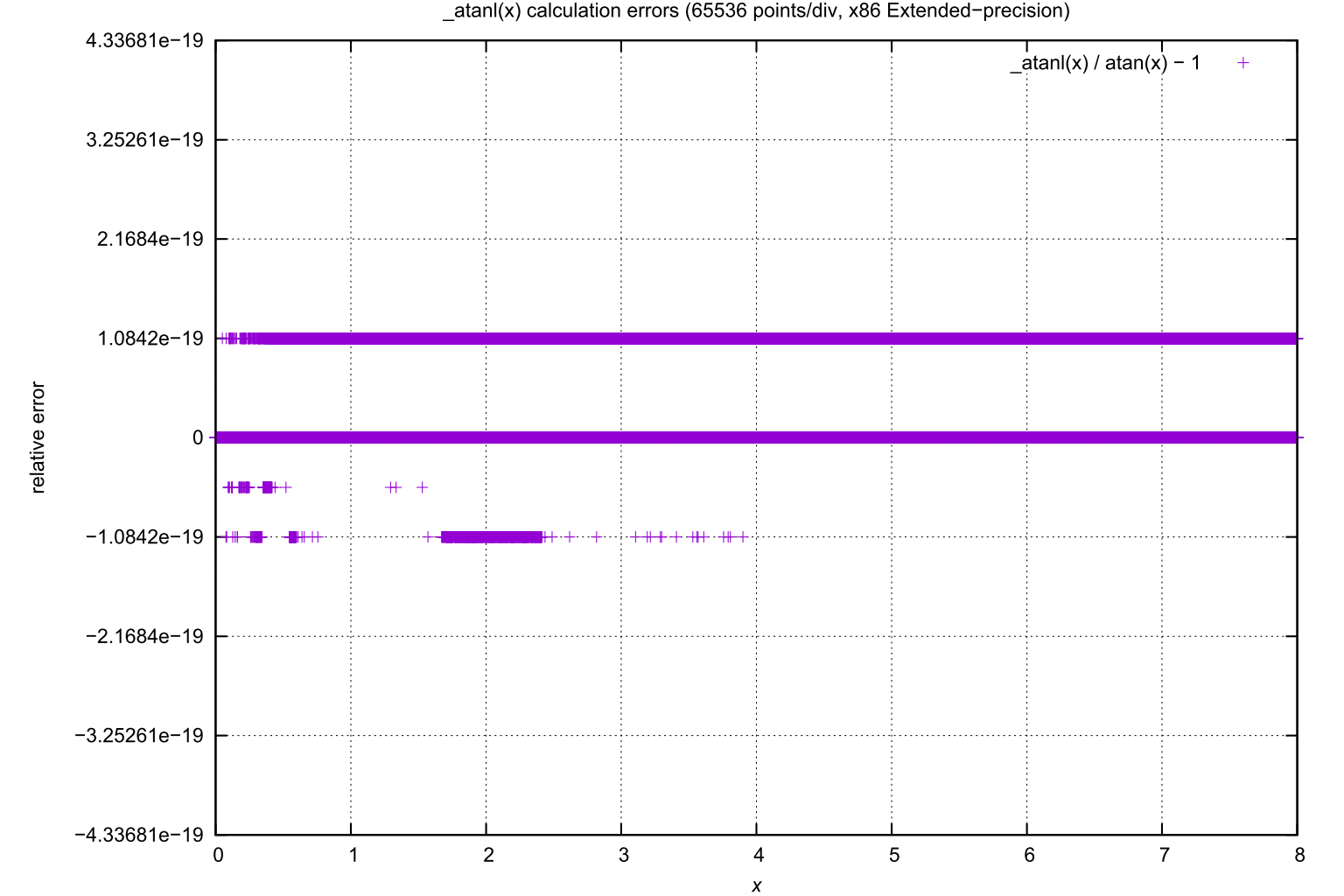
arc tangent calculation errors
Fig. 1: Relative error of _atanl(x), shown as _atanl(x) / atanref(x) - 1

Theoretical Approximation Error of the (14,14) Padé approximation

The theoretical approximation error of the (14,14) Padé approximation attains its maximum value of approximately -6.46×10-23 at x = √2 - 1.

The plot is calculated in a high-precision (≈40 digits) environment.

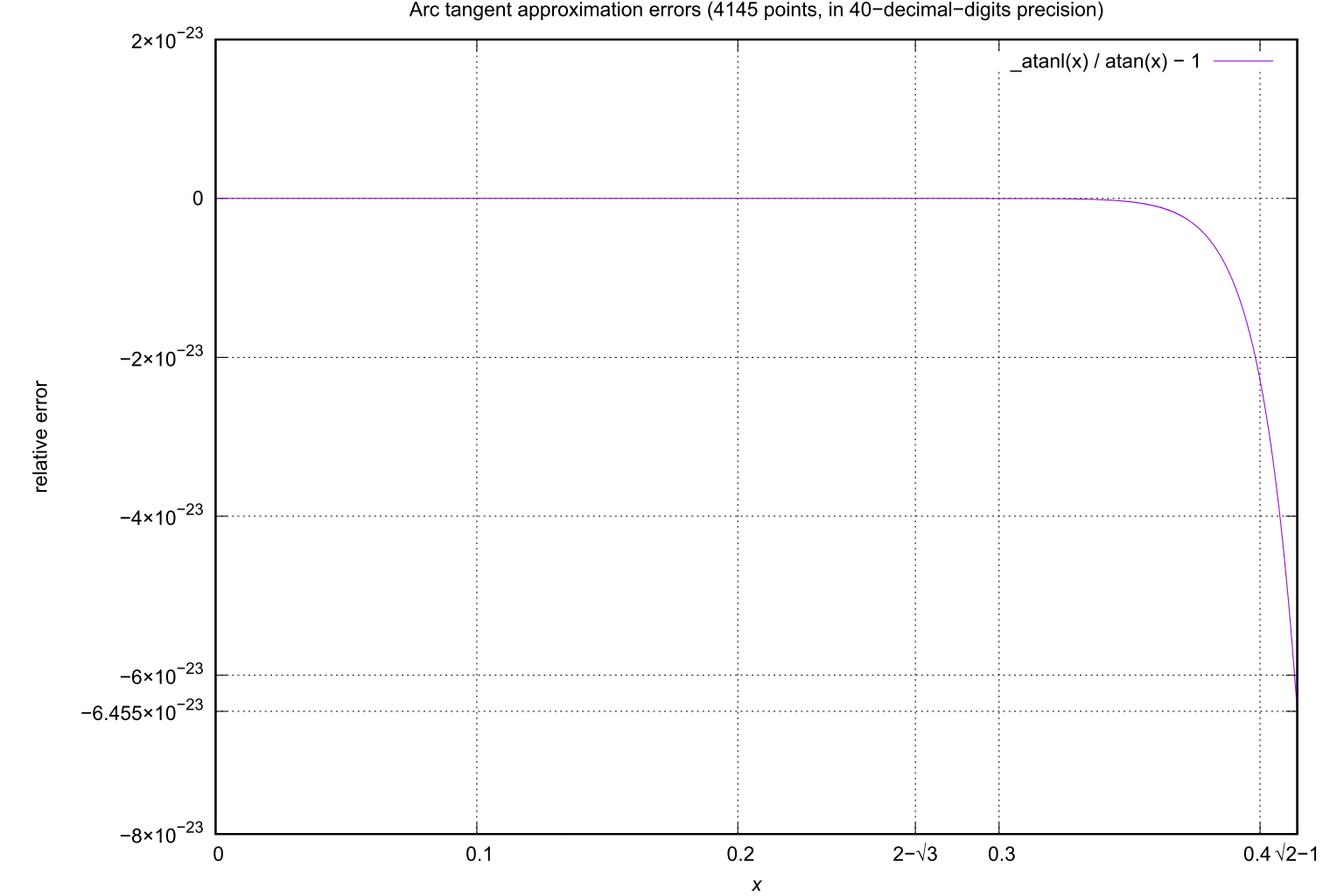
Theoretical arc tangent approximation errors
Fig. 2: Theoretical approximation error of the (14,14) Padé approximation used in _atanl(x)

Appendix A — IEEE 754 Double-Precision (64-bit)

_atan is a double-precision (64-bit) implementation of the arc-tangent function, derived from _atanl, the extended-precision version. To reduce the approximation error near the upper limit —where the error tends to be large in plain Padé approximations— some coefficients for higher-order terms are adjusted in a minimax-like manner. This makes it possible to use an approximation of order (8,10), instead of the (10,10) order required by a plain Padé approximation for double precision.

With a (10,10) plain Padé approximation, the maximum error is |error| < 3.86×10-17. In contrast, the (8,10) modified Padé approximation achieves a slightly better bound of |error| < 3.14×10-17 over the interval x ∈ [0, √2 - 1].

Listing 1: _atan — arc tangent function in C89 (ANSI-C) 
/* _atan -- arc tangent function in C89 (ANSI-C), IEEE 754 double-precision
 * _atan Rev.1.21 (Jan. 22, 2026) (c) 2007-2026 Takayuki HOSODA
 * SPDX-License-Identifier: BSD-3-Clause
 */
#include <math.h>
#include <float.h>

#ifndef M_SQRT2
#define M_SQRT2  1.41421356237309504880168872421
#endif
#ifndef M_PI_2
#define M_PI_2   1.57079632679489661923132169164
#endif
#ifndef M_PI_4
#define M_PI_4   0.78539816339744830961566084582
#endif
#ifndef DBL_EPSILON
#define DBL_EPSILON    2.2204460492503131E-16
#endif

double _atan(double x);
/* _atan(x)  computes the principal value of the arc tangent of x. */
double _atan(double x) {
    double q, s, v, w;
    double offset = 0;
    if (x == 0) return x;
    if (x >  (2 / DBL_EPSILON)) return  M_PI_2;
    if (x < -(2 / DBL_EPSILON)) return -M_PI_2;
    if ((v = fabs(x)) >= 1) {
        if (v > M_SQRT2 + 1) {
            offset = -M_PI_2; v = 1 / v;
        } else {
            offset =  M_PI_4; v = (v - 1) / (1 + v);
        }
    } else if (v >= M_SQRT2 - 1) {
            offset = -M_PI_4; v = (1 - v) / (1 + v);
    }  /* Argument reduction into four regions using atan identities */
    s = v * v;
    q =           2401244.6571; w =           2073564.8997;
    q = q * s +  52026974.7295; w = w * s +  32801340.0004;
    q = q * s + 312161850.;     w = w * s + 136306170.;
    q = q * s + 758107350.;     w = w * s + 205633428.;
    q = q * s + 800224425.;     w = w * s + 101846745.;
    q = q * s + 305540235.;     w = w * s;
    /* (8,10) modified Pade approximation for atan(x) / x - 1 */
    v -= w / q * v;  /* atan(x) = x - (atan(x) / x - 1) * x */
    s = v + offset;  /* |err| < 3.2e-17, x in [0, sqrt(2) - 1] */
    return (offset * x >= 0) ? (offset != 0 || x >= 0) ? s : -v : -s;
}

Empirical Error analysis (64-bit)

In an empirical evaluation conducted using GCC 7.5, the custom _atan function was tested on 65536 (= 216) uniformly spaced points per unit interval for x ∈ [0, 8] in double-precision values. The relative error, computed as _atan(x) / atanref(x) - 1 was found to be within ±2.2204460492503131E-16, approximately the machine epsilon for IEEE 754 double precision. Where atanref(x) denotes a rounded high-precision reference (≈ 40 digits), not a libm result.

For |x| > 8, argument reduction ensures that approximation errors rapidly diminish.

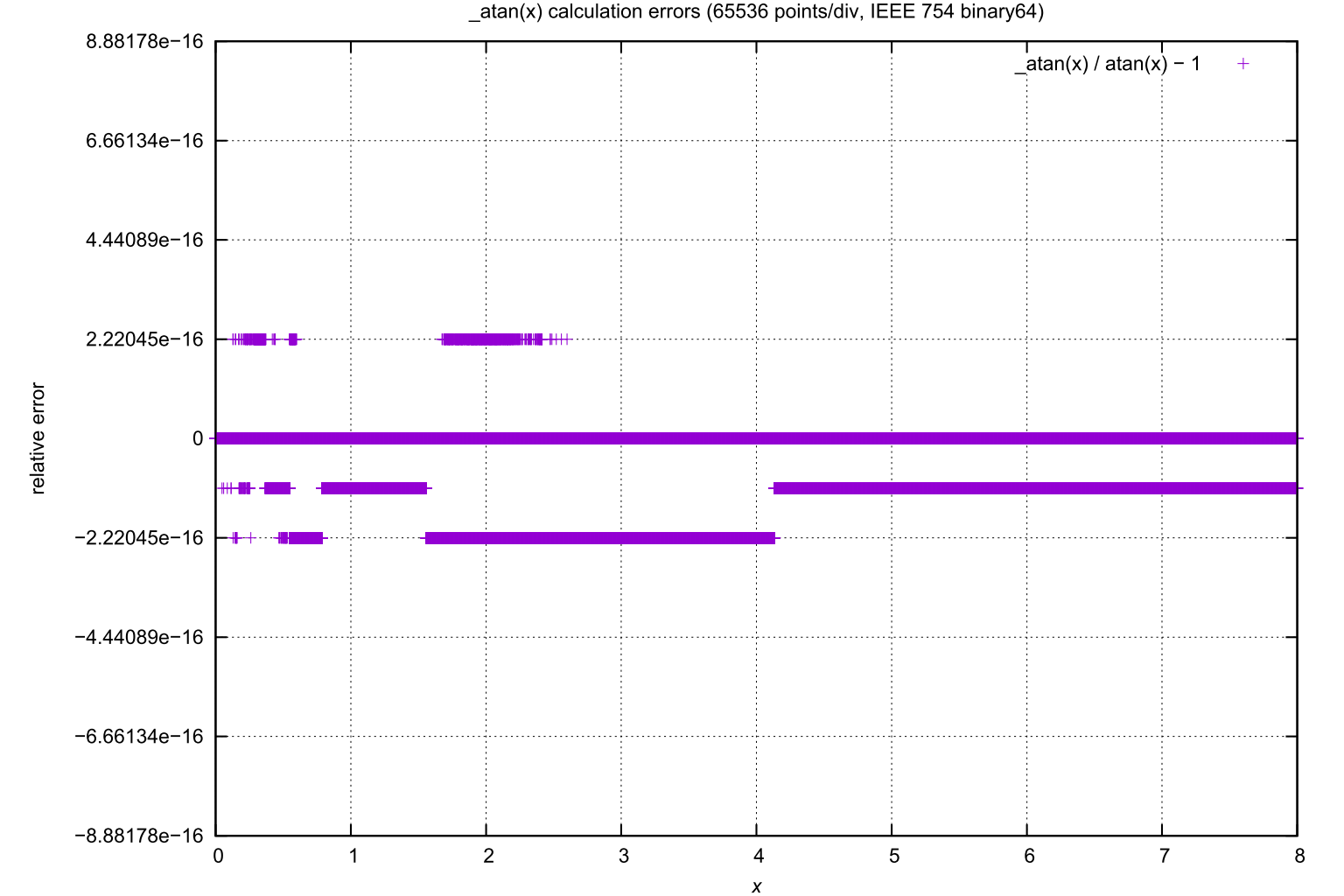
arc tangent calculation errors
Fig. 3: Relative error of _atan(x), shown as _atan(x) / atan(x) - 1, where atan(x) is a rounded high-precision reference (≈40 digits), not a libm result.

Theoretical Approximation Error (64-bit)

The theoretical approximation error of the (8,10) modified Padé approximation attains its maximum value of approximately -3.14×10-17 near x ≈ 0.4.

The plot is calculated in a high-precision (≈40 digits) environment.

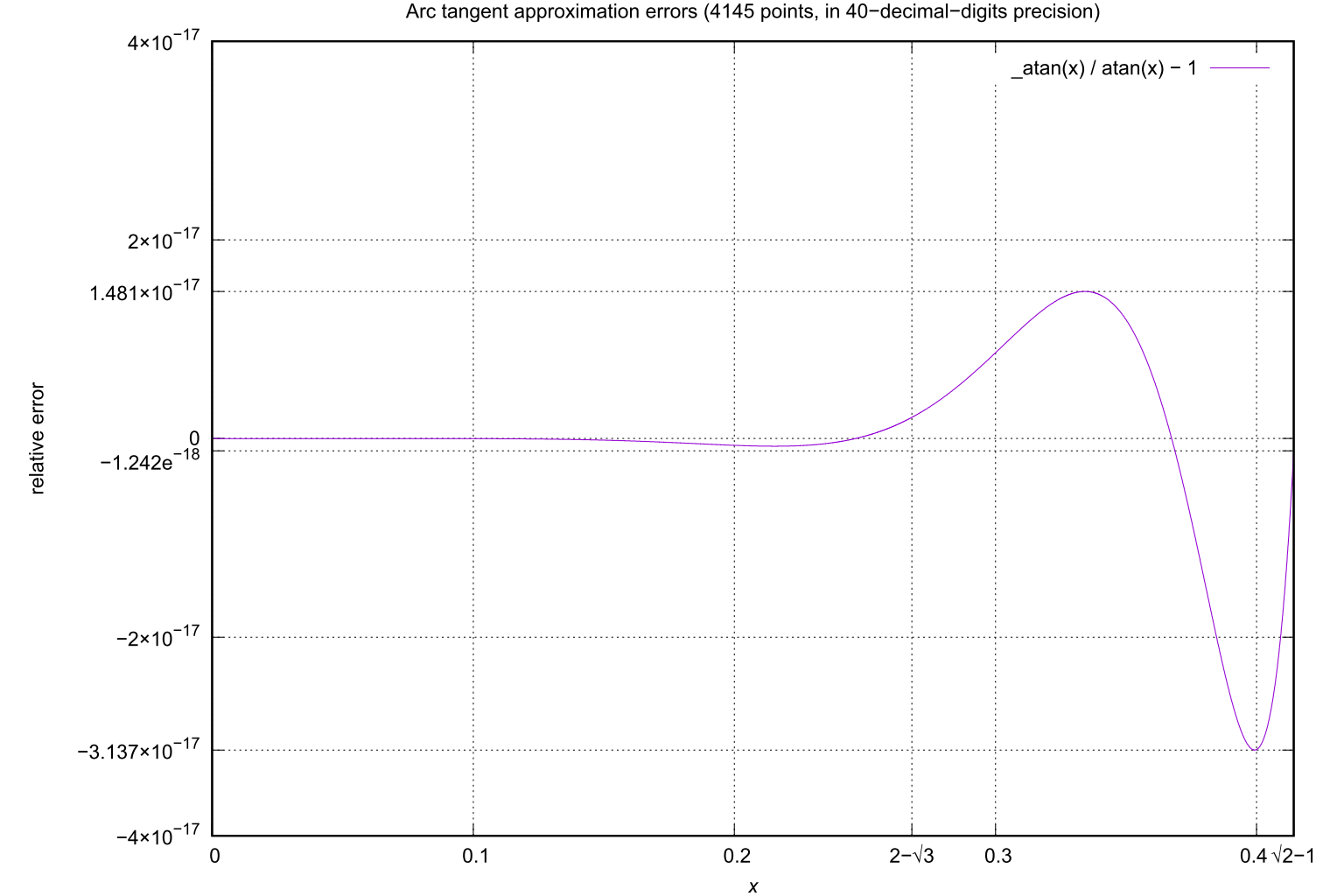
Theoretical arc tangent approximation errors
Fig. 4: Theoretical approximation error of the (8,10) modified Padé approximation used in _atan(x)

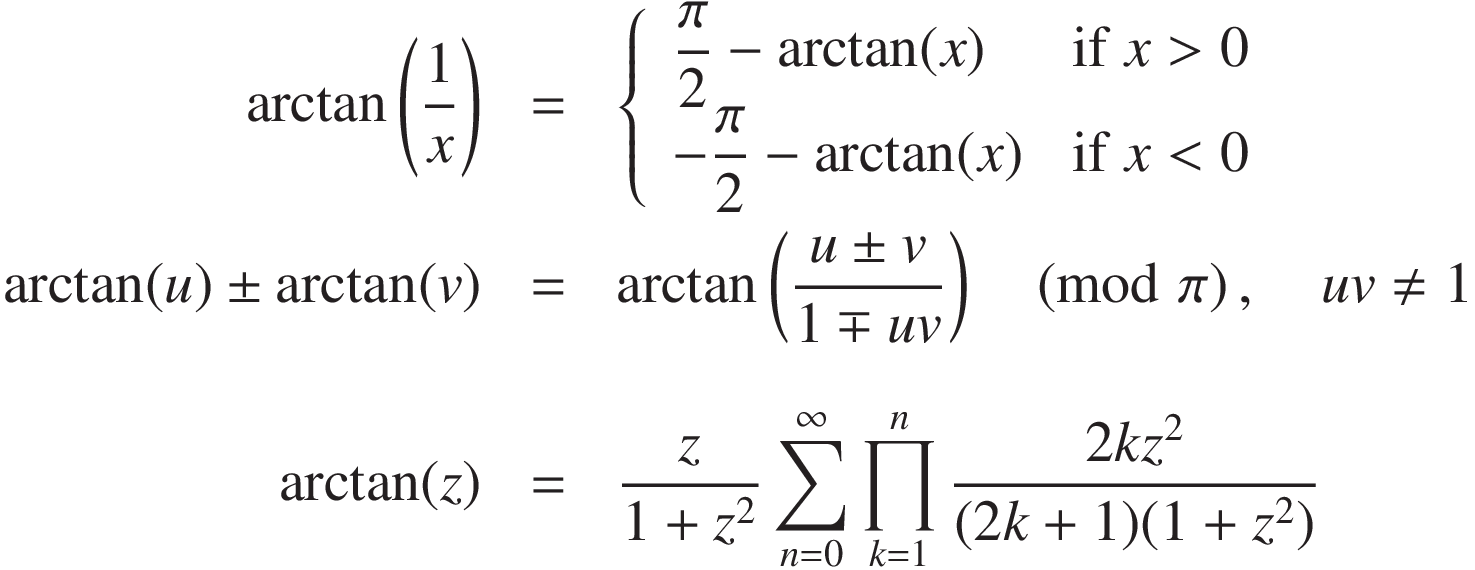
Appendix B — Identities and infinite series of the arctangent function

Identities and infinite series of the arctangent function

あとがき

長年にわたり、初期の 8 ビット CPU から現代の IEEE 754 システムに至るまでのハードウェアの進化を背景として、 テイラー近似、連分数近似、有理近似といったさまざまな手法が研究されてきました。

参考文献

Although not treated in the present implementation, the derivation of the inverse tangent function can also be formulated via elliptic functions and their inverse mappings. The following references 3–8 are cited for completeness.

  1. Jean-Michel Muller, Elementary Functions: Algorithms and Implementation, Birkhauser, 3rd Edition, 2016.
  2. Okumura, Haruhiko; Shudo, Kazuyuki; Sugiura, Masaki; Tsuchimura, Nobuyuki; Tsuru, Kazuo; Hosoda, Takayuki; Matsui, Yoshimitsu; & Mitsunari, Shigeo. (2003). Java ni yoru Arugorizumu Jiten [Encyclopedia of Algorithms with Java], Gijutsu Hyoron Sha, ISBN4-7741-1729-3 [in Japanese]
  3. N. I. Akhiezer, Elements of the Theory of Elliptic Functions, American Mathematical Society, Providence, RI, 1990. (Original Russian edition, 1970.)
  4. E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, 4th ed., Cambridge University Press, Cambridge, 1927.
  5. F. Bowman, Introduction to Elliptic Functions with Applications, Dover Publications, New York, 1961.
  6. A. Erdélyi et al., Higher Transcendental Functions, Vol. II, McGraw-Hill, New York, 1953.
  7. T. M. Apostol, Elliptic Functions and Modular Forms in Number Theory, Springer, New York, 1990.
  8. R. P. Brent, Fast Multiple-Precision Evaluation of Elementary Functions, Stanford Univ., Stanford, CA, USA, Tech. Rep. STAN-CS-75-515, Aug. 1975.

External links

www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.