in C99


Bessel filter calculation examples and design tables


Takayuk HOSODA
Apr. 11, 2024
Japanese Japanese edition is here.

Preface

It is now spring 2024, and Generative Pre-trained Transformers and cherry blossoms are in full bloom, I found a design table of active filters in the handbook of a technical magazine supplement. I know that flowers and GPTs are for viewing and not for use, but I was concerned because the design values for the Bessel filter [1][2] in the numerical table seemed to be "slightly" different.

I don't want to be serendipitous about it, but I was curious and did a bit of research. I couldn't trace the source of the table, but it seems to match the published values by about five digits when compared with the values calculated with the strict -3 dB cut-off frequency instead of √0.5, which seems like a total oversimplification (*1) The reason for about five digits is that the dawn of modern network theory in Japan was in the 1950s, and the original calculations may have been due to the single precision of the available computing environment.

In actual circuit design, pure Bessel filters are rarely employed, and even if they were, it is rare to design from a table of numbers now that a variety of design applications are available. However, there are also cases where a Bessel filter is required in terms of mathematical understanding and intrinsic nature, even if it is not a Bessel filter itself, from the point of view of error rates and EMC. For these reasons, this is a good opportunity to summarise the calculation examples, calculation programmes and design tables for Bessel filters once again.

Example calculation of a normalised Bessel filter

The transfer function of a third-order Bessel filter TBF(s, 3) can be approximated by a serial fraction expansion of the time delay transfer function [2][3] as follows

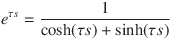
e^{ \tau s} = \frac{1}{\cosh( \tau s) + \sinh( \tau s)}
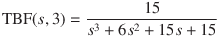
\mathrm{TBF}(s, 3) = \frac{15}{s^3 + 6 s^2 + 15 s + 15}

The cut-off frequency fc at which the absolute value of the amplitude of TBF(s, 3) is 1 / √2 is calculated as follows

fc = solve(abs(TBF(s, 3), s) - sqrt(0.5) → fc ≃ 1.75567236868121064920

Where solve(f(s), s) means solve (*2) the function f(s) for s.

The normalised transfer function TBFN(s, 3) of the third-order Bessel filter normalised by fc approximately becomes

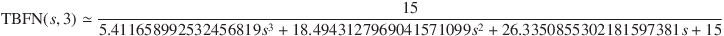
\mathrm{TBFN}(s, 3) \simeq \frac{15 }{5.411658992532456819 s^3 + 18.4943127969041571099 s^2 + 26.3350855302181597381 s + 15}

The poles p of TBFN(s, 3) are obtained by solving the denominator as follows.

solve(15 / TBFN(s, 3), s) → p ≃ {-1.322675800, -1.047409161 ± i 0.9992644365 }

The natural frequency ω and quality factor Q for one pole p of p are defined as follows

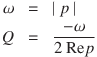
\omega &=& |\ p\ |\\Q &=& \frac{-\omega}{2\ \mathrm{Re}p}

Therefore, the normalised design parameters for a third-order Bessel filter in a two-stage configuration are calculated as follows

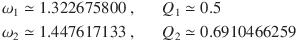
\omega_1 \simeq 1.322675800\ ,&& Q_1 \simeq 0.5\\ \omega_2 \simeq 1.447617133\ ,&& Q_2 \simeq 0.6910466259

Appendix

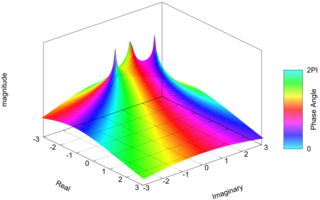
Frequency versus amplitude characteristics of the normalised Bessel filters (1st to 12th order)

fig.1 Frequency response of the normalized Bessel filters (1st - 12th order)
Results of SPICE3 simulations of the normalised Bessel filters (1st to 12th order)
Group delay of the normalized Bessel filters
fig.2 Group delay characteristics of the normalized Bessel filters (1st to 12th order)
AC simulation results of the normalised Bessel filter of active filters with ideal op-amps using SPICE3.

Transcient response of the normalized Bessel filters
fig.3 Transcient response of the normalized Bessel filters (1st to 12th order)
TRAN simulation results of the normalised Bessel filter of active filters with ideal op-amps using SPICE3.
The transfer function of the Bessel filters (1st to 12th order)
\mathrm{TBF}(s, n) = \displaystyle\frac{\displaystyle\frac{(2n)!}{n!\ 2^n}} {\displaystyle\sum _{k=0}^{n}{\displaystyle\frac {(2n - k)!}{(n-k)!\ k!}}\,s^k}
\mathrm{TBF}(s,1)&=&\frac{1}{s+1}\\ \mathrm{TBF}(s,2)&=&\frac{3}{s^2+3s+3}\\ \mathrm{TBF}(s,3)&=&\frac{15}{s^3+6s^2+15s+15}\\ \mathrm{TBF}(s,4)&=&\frac{105}{s^4+10s^3+45s^2+105s+105}\\ \mathrm{TBF}(s,5)&=&\frac{945}{s^5+15s^4+105s^3+420s^2+945s+945}\\ \mathrm{TBF}(s,6)&=&\frac{10395}{s^6+21s^5+210s^4+1260s^3+4725s^2+10395s+10395}\\ \mathrm{TBF}(s,7)&=&\frac{135135}{s^7+28s^6+378s^5+3150s^4+17325s^3+62370s^2+135135s+135135}\\ \mathrm{TBF}(s,8)&=&\frac{2027025}{s^8+36s^7+630s^6+6930s^5+51975s^4+270270s^3+945945s^2+2027025s+2027025}\\ \mathrm{TBF}(s,9)&=&\frac{34459425}{s^9+45s^8+990s^7+13860s^6+135135s^5+945945s^4+4729725s^3+16216200s^2+34459425s+34459425} \mathrm{TBF}(s,10)&=&\frac{654729075}{s^{11}+55s^9+1485s^8+25740s^7+315315s^6+2837835s^5+18918900s^4+91891800s^3+310134825s^2+654729075s+654729075}\\ \mathrm{TBF}(s,11)&=&\frac{13749310575}{s^{11}+66s^{10}+2145s^9+45045s^8+675675s^7+7567560s^6+64324260s^5+413513100s^4+1964187225s^3+6547290750s^2+13749310575s+13749310575}\\ \mathrm{TBF}(s,12)&=&\frac{316234143225}{s^{12}+78s^{11}+3003s^{10}+75075s^9+1351350s^8+18378360s^7+192972780s^6+1571349780s^5+9820936125s^4+45831035250s^3+151242416325s^2+316234143225s+316234143225}
The cut-off frequency of the Bessel filters (1st to 12th order)
\mathrm{order} && \mathrm{cut-off\; frequency}\\ n && f_c\\ 1 && 1.00000000000000000000\\ 2 && 1.36165412871613052096\\ 3 && 1.75567236868121064920\\ 4 && 2.11391767490421584302\\ 5 && 2.42741070215262813767\\ 6 && 2.70339506120292187640\\ 7 && 2.95172214703872277193\\ 8 && 3.17961723751065133050\\ 9 && 3.39169313891166010111\\ 10 && 3.59098059456916348279\\ 11 && 3.77960741643962009289\\ 12 && 3.95915082114428531554
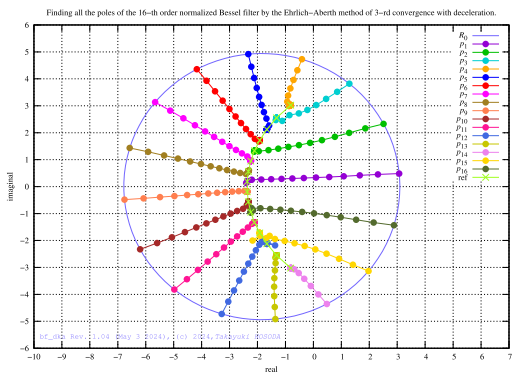
Poles of the normalised Bessel filter (2nd to 12th order)
\xi_\mathrm{Bessel}(2) \simeq &&\{-1.1016013305921617015 \pm i\ 0.63600982475703448213\}\\ \xi_\mathrm{Bessel}(3) \simeq &&\{-1.3226757999104447673,\\ &&\; -1.0474091610089354263 \pm i\ 0.99926443628063757599\}\\ \xi_\mathrm{Bessel}(4) \simeq &&\{-1.3700678305514442327 \pm i\ 0.410249717493752057,\\ &&\; -0.99520876435027351019 \pm i\ 1.2571057394546661002\}\\ \xi_\mathrm{Bessel}(5) \simeq &&\{-1.5023162714474789878,\\ &&\; -0.95767654856268193176 \pm i\ 1.471124320730395064,\\ &&\; -1.3808773258604395854 \pm i\ 0.71790958762676845074\}\\ \xi_\mathrm{Bessel}(6) \simeq &&\{-1.3818580975965633864 \pm i\ 0.97147189071157097218,\\ &&\; -0.93065652294685864233 \pm i\ 1.6618632689425906009,\\ &&\; -1.5714904036160307848 \pm i\ 0.32089637422262373156\}\\ \xi_\mathrm{Bessel}(7) \simeq &&\{-1.684368179273180171,\\ &&\; -0.90986778062346975444 \pm i\ 1.8364513530363928286,\\ &&\; -1.3789032167954738438 \pm i\ 1.1915667778006519794,\\ &&\; -1.6120387662261241751 \pm i\ 0.58924450693147147295\}
\xi_\mathrm{Bessel}(8) \simeq &&\{-1.636939418126879603 \pm i\ 0.82279562513969530055,\\ &&\; -0.8928697188471322178 \pm i\ 1.9983258436412952024,\\ &&\; -1.3738412176373695236 \pm i\ 1.3883565758775552145,\\ &&\; -1.7574084004016431415 \pm i\ 0.27286757510223119062\}\\ \xi_\mathrm{Bessel}(9) \simeq &&\{-1.8566005012280034477,\\ &&\; -1.6523964845788349908 \pm i\ 1.031389566984410613,\\ &&\; -0.87839927616095252348 \pm i\ 2.1498005243133215095,\\ &&\; -1.80717053496210115 \pm i\ 0.5123837305749040137,\\ &&\; -1.3675883097929051509 \pm i\ 1.5677337122372686999\}\\ \xi_\mathrm{Bessel}(10) \simeq &&\{-1.360692278384544035 \pm i\ 1.7335057426614761842,\\ &&\; -1.8421962445248344952 \pm i\ 0.72725759775747787213,\\ &&\; -1.9276196913722768577 \pm i\ 0.24162347097153336661,\\ &&\; -0.86575690170837525248 \pm i\ 2.2926048309824757853,\\ &&\; -1.6618102413621520203 \pm i\ 1.2211002185791613521\}
\xi_\mathrm{Bessel}(11) \simeq &&\{-2.0167014734500268025,\\ &&\; -1.6671936422452973207 \pm i\ 1.3959629036464656916,\\ &&\; -1.3534866773880991371 \pm i\ 1.8882968447597186611,\\ &&\; -1.8673612388872039264 \pm i\ 0.92311558295185904374,\\ &&\; -1.9801606453037554436 \pm i\ 0.45959874382661401508,\\ &&\; -0.85451258135234993207 \pm i\ 2.4280594669150566409\}\\ \xi_\mathrm{Bessel}(12) \simeq &&\{-0.84437887285039650684 \pm i\ 2.5571889692029125806,\\ &&\; -1.8856496197318523848 \pm i\ 1.1038148812152310505,\\ &&\; -1.6698035888528286074 \pm i\ 1.5588027008411653863,\\ &&\; -2.0199459330751226282 \pm i\ 0.65899650071722267946,\\ &&\; -1.3461746802905127508 \pm i\ 2.033998508278489405,\\ &&\; -1.0846445069315783593 \pm i\ 0.21916153518975516035\}
poles-of-the-normalized-bessel-filters.png
fig.4 Poles of the normalized Bessel filters (1st - 16th order)
Poles are connected by lines for each group.

Note

*1 : By definition, the cut-off frequency is the frequency at which the transferred power is halved, since it is 1/√2 ≃ -3 dB (i.e. 10-3/20 / (1/√2) - 1 ≃ 0.0011865297 ). In radio engineering, an error of about 0.1 % is negligible, but in the case of numerial tables it is a different story.

*2 : The Newton-Raphson method, Ostrowski's method [4][5] and others are used for solving equations, DKA (Durand-Kerner-Aberth) method [4] [6] [9] and others are used for solving higher-order algebraic equations.

Source code (C99)

bf_dka -- A solver for reverse Bessel polynomials using the Durand-Kerner-Aberth method.

bf_dka.c ◆ click to unfold/fold
\widehat{x_i} &=& x_i - \frac{{p_n(x_i)}}{{{p'_n(x_i)} - {p_n(x_i)} \displaystyle\sum_{\substack{j = 0\\j \neq i}}^ {n-1} \frac{1}{x_i - x_j}}}

Conclusion

I tried to find some textbooks and practical books related to analogue filters, but... I haven't been able to find an "accurate" table of 8+ digit numbers with a basis for calculations. There are a number of excellent CAS (Computer Algebra Systems) available nowadays, but I tried again to see how far I could get with C99 double-precision complex numbers and 64-bit integers. Unlike CAS, when you write in C, you can keep all the algorithms and optimisations for the limits of the computer in your hands, so I'm glad to be able to use it for other purposes. The results from the above program which uses the DKA (Durand-Kerner-Aberth) method were valid up to 11 digits for the 12th order, 9 digits for the 16th order and up to 8 digits for the 17th order in comparison with the maximum absolute value of the relative error to the reference value calculated to 25-digit precision in CAS.

bf-dka-errors.png
fig.5 Maximum error V.S. order (Ehrilich-Aberth and Durand-Kerner method)

Appendix

Design table for normalised Bessel filters (2nd to 17th order)
ormalized-bessel-filter-design-parameters
  normalized-bessel-filter-design-parameters-1.31.pdf
Bessel filter simulation circuit example (3rd order, VCVS type, for LTspice)
bessel3-sch
bessel3-tr
 bessel3-ltspice.zip

References

  1. G.N.Watson. A TREATISE ON THE THEORY OF BESSEL FUNCTIONS. SECOND EDITION. Cambridge University Press, 1966, 815p
  2. Thomson, W.E. "Delay networks having maximally flat frequency characteristics", Proceedings of the IEE - Part III: Radio and Communication Engineering, 1949, 96, (44), p. 487-490
  3. Akio Katsumada "About the automatic design of Bessel digital filters" Seismic Test Report Vol. 56, 1993, p. 17-34
  4. Hayato Togawa "Scientific and Technical Computing Handbook", Science Publishing, Tokyo, 1992, ISBN 4-7819-0666-4
  5. .M.Ostrowskis. SOLUTION OF EQUATIONS IN EUCLIDEAN AND BANACH SPACES. THIRD EDITION. Academic Press, New Yoark and London, 1973
  6. Tetsuro Yamamoto, Utaro Furukane, Kumi Nokura "Durand-Kerner method and Aberth method for solving algebraic equations", Information Processing Vol.18 No.6 June 1977, p. 566-571
  7. Tsuneo Shiraki, Takao Terano, Hideharu Nakamura, and Chizuko Kurihara, "Solution of transcendental equations using the DKA method and its application examples," Proceedings of the Japan Society of Civil Engineers, No. 416/1-13, 1990, p. 295-302
  8. Edited by Ryo Natori, co-authored by Hidehiko Hasegawa, Tetsuya Sakurai, Sumiko Hiyama, et al., "Numerical Calculation Method", Ohmsha, Tokyo, Japan, 1998.9, p.109-113, ISBN 4-274-13153-X
  9. Kazufumi Ozawa, "Simple method for setting efficient initial values ??of the Durand-Kerner method", Transactions of the Japan Society of Applied Mathematics Vol.3, No.4, 1993, p.173-186

See Also

External Links

www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.