in C
An implementation of
Complete Elliptic Integral of the First Kind

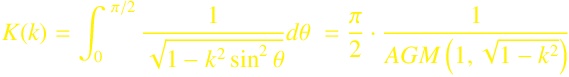
K(k) = \int_0^{\ \pi / 2} \frac{1}{ \sqrt{1 - k^2 \sin^2 \theta }} d \theta \ = \frac{ \pi }{2} \cdot \frac{1}{AGM\left(1, \sqrt{1 - k^2}\right)}

Dec. 17 2022
Takayuki HOSODA

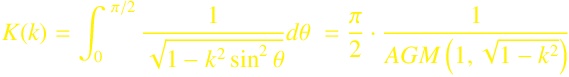
The calculation is performed using the relationship between Complete Elliptic Integrals of the First Kind and the Arithmetic Geometric Mean.

EllipticK.c
NAME
    _elliptick -- returns the complete elliptic integral of the first kind. 

LIBRARY
    Math library (libm, -lm)\n\

SYNOPSIS
    #include <math.h>

    double
    _elliptick(double k);

RETURN VALUE
    _elliptick(k) returns the complete elliptic integral of the first kind K(k) | (-1 < k < 1).

/* _elliptickk - The complete elliptic integral of the first kind function written for C 
  by Takayuki HOSODA (aka Lyuka). Rev. 0.3 (Dec. 17, 2022) 
  _elliptick(k) returns the complete elliptic integral of the first kind K(k) | (-1 < k < 1) 
  K(k) = \int_0^{\pi / 2} \frac{1}{ \sqrt{1 - k^2 \sin^2  \theta }} d \theta 
*/
#include <math.h>
#ifndef DBL_EPSILON
#define DBL_EPSILON     2.2204460492503131E-16
#endif
#ifndef M_PI
#define M_PI            3.14159265358979323846
#endif

double
_elliptick(double k) {
    double b, e, a, m;
    a = 1.0;
    e = 4.0 * DBL_EPSILON;
    m = k * k;
    b = sqrt(a - m);
    do  {
        m = 0.5 * (a + b);
        b = sqrt(a * b);
        a = m;
    } while (fabs(a / b - 1.0) > e);
    return M_PI / (a + b);
}
#ifdef DEBUG
#include <stdio.h>
#include <stdlib.h>
double _elliptick(double);
char * help = "Name\n\
    _elliptick(k) returns the complete elliptic integral of the first kind K(k) | (-1 < k < 1).\n";
char * example = "EXAMPLE\n\
    _elliptick(0.5) = 1.685750354812596\n";
int
main(int argc, char *argv[]) {
    double k;

    if (argc == 2) {
        k = atof(argv[1]);
        if (fabs(k) < 1) { 
            printf("_elliptick(%.16g) = %.16g\n", k, _elliptick(k));
        } else {
            fprintf(stderr, "%s : Domain error. The domain of the argument k is -1 < k < 1.0.\n", argv[0]);
        }
    } else {
        printf("%s\n%s", help, example);
    }
    return(0);
}
#endif
EllipticK — The complete elliptic integral of the first kind. Rev.0.3 (Dec. 17, 2022) (c) 2022 Takayuki HOSODA

Calculation example of _elliptick()

_elliptick(0.1) = 1.574745561517356
_elliptick(0.2) = 1.586867847454166
_elliptick(0.3) = 1.608048619930513
_elliptick(0.5) = 1.685750354812596
_elliptick(0.7) = 1.845693998374724
_elliptick(0.9) = 2.28054913842277

Calculation results by WolframAlpha

K(0.12) = 1.5747455615173559526690306886598600916467487899161313721057468275...
K(0.22) = 1.5868678474541662373080080338281141929509961107345646882161300510...
K(0.32) = 1.6080486199305128012672072222386871571121767288026525584963492535...
K(0.52) = 1.6857503548125960428712036577990769895008008941410890441199482978...
K(0.72) = 1.8456939983747235175865286548842198353181604236409512574723010655...
K(0.92) = 2.2805491384227702046137519445555304387432379662787933369283410637...

SEE ALSO

www.finetune.co.jp [Mail] © 2000 Takayuki HOSODA.